(2021.10.07)
알고리즘 수업들으면서 정리하기 4탄
3주차 내용
Merge Sort
insertion sort가 incremental approach로 정렬하는 반면, (정렬된 배열의 원소개수가 늘어남)
merge sort는 divide-and conquer approach로 정렬한다.
--> divide-and-conquer approackh는 recursion의 개념을 기반으로 한다.
Divide-and-conquer
- Divide the problem into several su-bproblems
- Conquer the sub-problems by solving them recursively.
- Combine the solutions to the sub-problems to get the solution for the original problem.
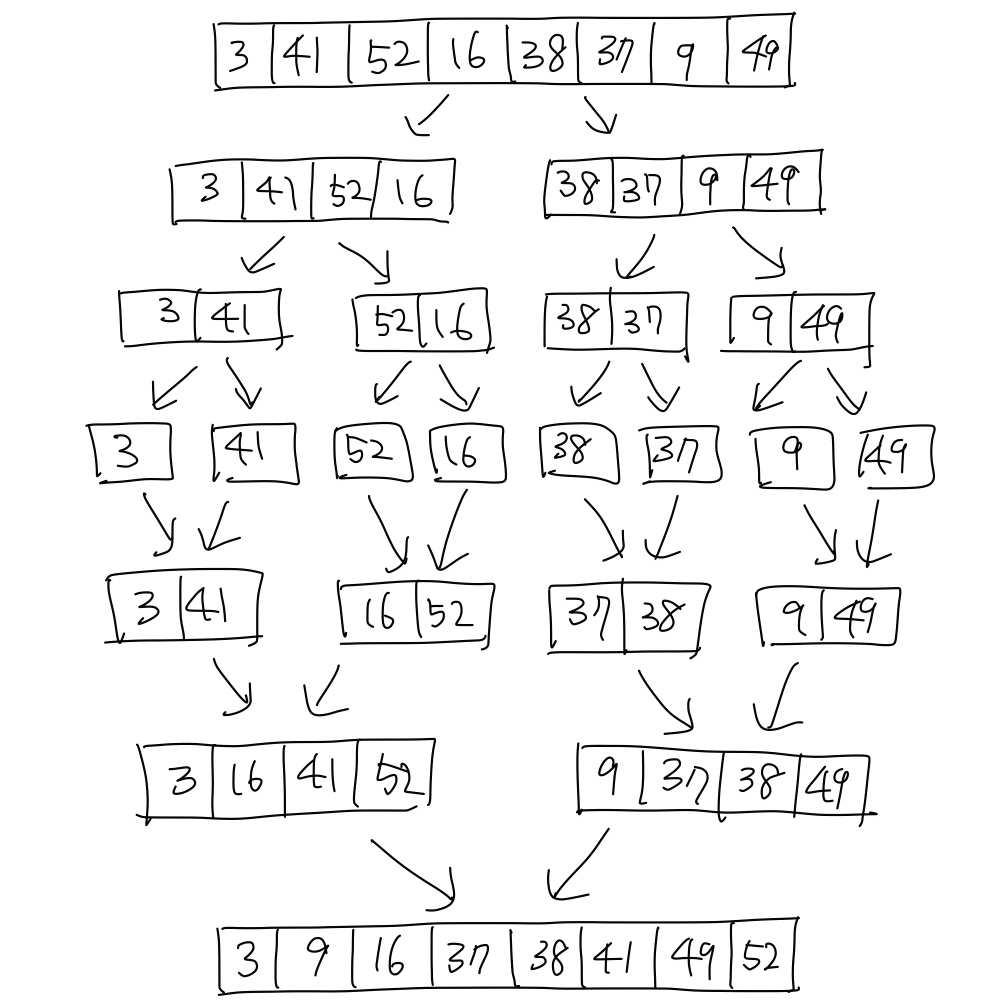
merge sort에서 divide-and-conquer
- Divide the n-element sequence to be sorted into two sub-sequences of n/2 each
- Conquer by sorting the sub-sequences recursively by calling merge sort agian (sub-sequence 길이가 1이 되면 이미 정렬된 것으로 취급)
- Combine the two sub-sequences by merging them to get a sorted sequence
def mergesort(l):
if len(l)<2:
return 1
mid=len(l)//2
left=mergesort(l[:mid])
right=mergesort(l[mid:])
return merge(left,right)
l=[3, 41, 52, 16, 38, 37, 9, 49]
void merge(char left, char right, char A, int l. int r){
int a,b=1;
for(int i=0;i<l+r;i++){
if left[a] <= right[b]{
A[i]=left[a];
a=a+1;
}
else {
A[i]=right[b];
b=b+1;
}
}
}
merge sort - loop invariants
statement:
1) A[p...k-1]까지의 배열은 L[q...n1+1]과 R[1...n2+1]의 (k-1)-p+1=k-p 개의 요소들이 작은 순서대로 정렬된 것이다.
2) L[i]와 R[i]는 각각의 배열에서 가장 작은 수를 가리킨다.
Initialization(초기조건): k=p인데, A[p...k-1]은 비어있음을 알 수 있고, k-p=0이므로 배열 A는 L과 R의 0번째까지 작은 원소를 가진다. 그리고, i=j=1 이므로 L[1]과 R[1]은 각각 가장 작은 수이다.
Maintenance(유지조건): 배열 A[k]이서 A[p]부터 A[k-1] 까지 (k-1-p+1)=k-p 개는 이미 정렬되어있다.
- 만약 L[i]≤R[i] 이면, L[i]는 A에 속하지 않은 것 중 가장 작고, L[i]를 A에 넣으면, A[p...k]는 정렬된다. (k-p+1) 번째로 작은 수까지 정렬되어있는 것이다. 그 이후에는 k와 i를 1씩 늘리고, 계속해서 진행한다.
- 만약 L[i]≥R[i] 이면, R[i]는 A에 속하지 않은 것 중 가장 작고, R[i]를 A에 넣으면, A[p...k]는 정렬된다. (k-p+1) 번째로 작은 수까지 정렬되어있는 것이다. 그 이후에는 k와 i를 1씩 늘리고, 계속해서 진행한다.
Termination(종료조건): k=r 일 때까지 반복하다가 k=r+1일 때 끝난다. k=r+1, r=k-1, A[p...k-1]에서 k-1=r 이르모 A[p...r]까지 정렬되었다고 할 수 있다. n1+n2=(q-p)+1 +(r-q)=r-p+1 인데 이는 A[p...r]에서 배열요소의 개수 r-p+1과 같다.
'Computer Science > algorithms' 카테고리의 다른 글
| [알고리즘] Maximum-subarray problem: divide-and-conquer (0) | 2021.10.08 |
|---|---|
| [알고리즘] Divide-and-Conquer algorithms & master method for solving recurrences (0) | 2021.10.07 |
| [알고리즘] Asymptotic Notation (0) | 2021.10.07 |
| [알고리즘] insertion sort - loop invariants & runtime (0) | 2021.10.06 |
| [알고리즘] insertion sort - 작동원리 (1) | 2021.10.06 |
