(2021.10.06)
알고리즘 수업들으면서 정리하기 2탄
2주차+3주차 내용
Insertion sort - loop invariants
statement: j-1 번째까지는 정렬되어 있음이 계속 보장된다.
Initialization(초기조건): first iteration 전에도 참이어야 하는데, j=2부터 시작되는 것을 통해 first iteration 전에는 j=1임을 생각할 수 있다. j=1 일 때, A[1]은 원소가 하나이기 때문에 정렬 상태이므로 참이다.
Maintenance(유지조건): 한 iteration이전에 참이었다면, 다음 iteration 이전에도 참을 유지해야 하는데, inner loop에 들어가기 전에는 out of order이고, loop를 나오는 순간에 key값이 order가 맞는 위치로 삽입되어 correct order가 된다.
Termination(종료조건): loop가 종료되었을 때, 알고리즘이 정확한지를 효과적으로 도출해 내야하는데 j=n+1 이면, loop는 종료된다. 항상 j-1번째까지는 정렬되어 있으므로, j-1=n 즉 A[1~n]까지는 정렬된 상태임을 알 수 있다.
Insertion sort - running time
- pseudocode에서 line 한 줄의 cost를 cn이라고 둔다. (첫번째 라인은 c1, 두번째 라인은 c2)
- print문 같은 loop가 아닌 line일 때의 running time은 그냥 더한다. (c1+c2)
- loop가 아닌 (loop가 없는) 알고리즘의 running time은 a constant 시간이다. (그냥 상수)

- cost는 상수값임. 알고리즘의 한 줄을 수행하는 operation의 computation cost를 가리킴.
- times는 알고리즘의 특정한 한 줄을 수행하는 횟수를 의미함.
- tj는 loop가 시행되는 횟수를 의미함.

insertion sort는 input에 의존한다.
input이 이미 정렬된 배열이면, insertion sort를 하는데 iteration(비교 횟수)이 줄어든다.
--> 즉, sorted input과 unsorted input에 따라 runtime이 차이가 난다.
input size에 따라서도 차이가난다.
insertion sort의 BEST case runtime

insertion sort의 WORST case runtime

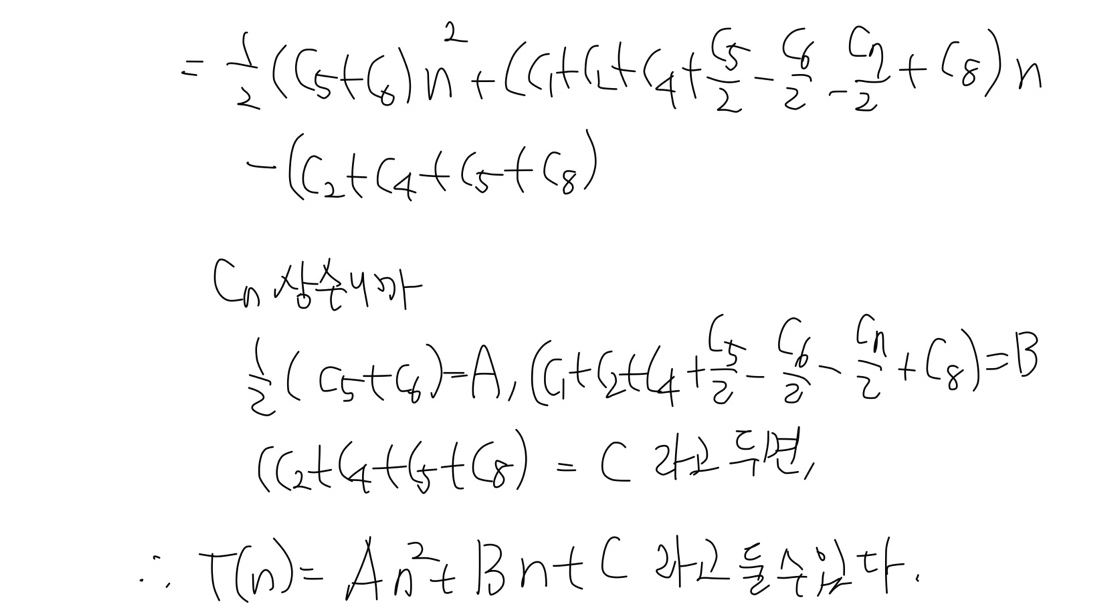
'Computer Science > algorithms' 카테고리의 다른 글
| [알고리즘] Maximum-subarray problem: divide-and-conquer (0) | 2021.10.08 |
|---|---|
| [알고리즘] Divide-and-Conquer algorithms & master method for solving recurrences (0) | 2021.10.07 |
| [알고리즘] Merge sort: divide-and-conquer & loop invariants (0) | 2021.10.07 |
| [알고리즘] Asymptotic Notation (0) | 2021.10.07 |
| [알고리즘] insertion sort - 작동원리 (1) | 2021.10.06 |
