(2021.10.08)
알고리즘 수업들으면서 정리하기 6탄
5주차 내용 -1 (4주차는 추석이어서 수업 없었음)
Maximum-subarray problem
input: sequence of numbers A[1 ... n]
output: subarray의 greatest sum(contiguous subarray of A) A[i ... j]
Naive approach
교수님께서 어떠한 문제를 풀 때는 naive하게 풀어보는 것부터 시작해보라고 하셨다
(naive 뜻을 몰라서 처음엔 무슨 말인지 이해하지 못했음)

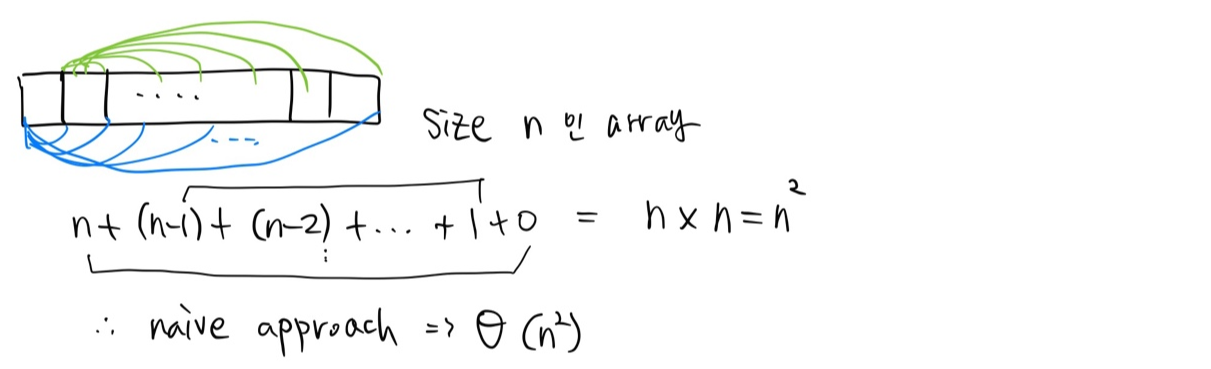
Divide-and-conquer approach
- Subproblem: Find a maximum subarray of A[low..high] (original call low=1, high=n)
- Divide the subarray into two subarrays (가능한 같은 사이즈로) Find the mid point (mid) of the subarrays
- Conquer by finding a maximum subarrays of A[low..mid] and A[mid+1..high]
- Combine by finding a maximum subarray that crosses the midpoint and using the best solution out of the three
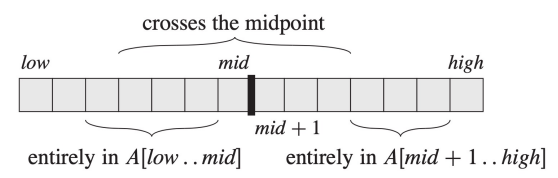
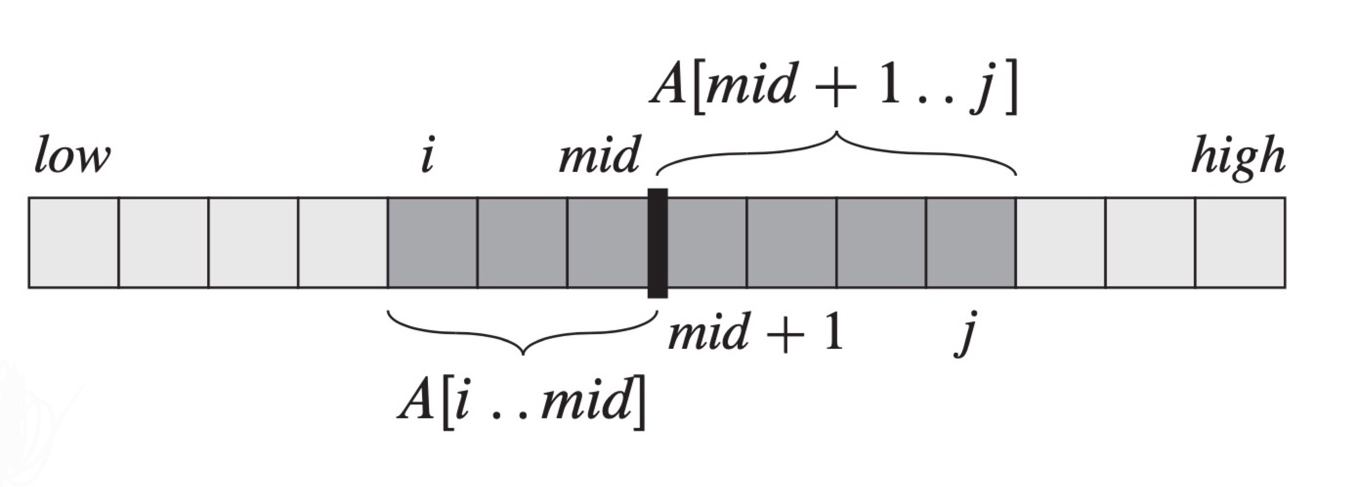
mid를 포함하는 maximum subarray 는 A[i..mid]와 A[mid+1..j]로 만들어진다
low≤i≤mid , mid<j≤high 를 만족한다
//main algorithm
FIND-MAXIMUM-SUBARRAY(A,low,high)
if high==low
return (low, high, A[low]) // base case: only one element
else
mid=(low+high)/2
(left-low,left-high,left-sum) = FIND-MAXIMUM-SUBARRAY(A,low,mid)
(right-low,right-high,right-sum) = FIND-MAXIMUM-SUBARRAY(A,mid+1,high)
(cross-low,cross-high,cross-sum) = FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)
if left-sum>=right-sum and left-sum>=cross-sum
return (left-low,left-high,left-sum)
else if right-sum>=left-sum and right-sum>=cross-sum
return (right-low,right-high,right-sum)
else
return (cross-low,cross-high,cross-sum)
FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)
left-sum=-∞
sum=0
for i=mid downto low
sum=sum+A[i]
if sum>left-sum
left-sum=sum
max-left=i
right-sum=-∞
sum=0
for j=mid+1 to high
sum=sum+A[j]
if sum>tight-sum
right-sum=sum
max-right=j
return (max-left,max-right,left-sum + right-sum)
Divide-and-conquer를 이용한 Maximum-subarray 의 T(n) 계산
Initial call: FIND-MAX-CROSSING-SUBARRAY(A,1,n)
--> low=1, high=n
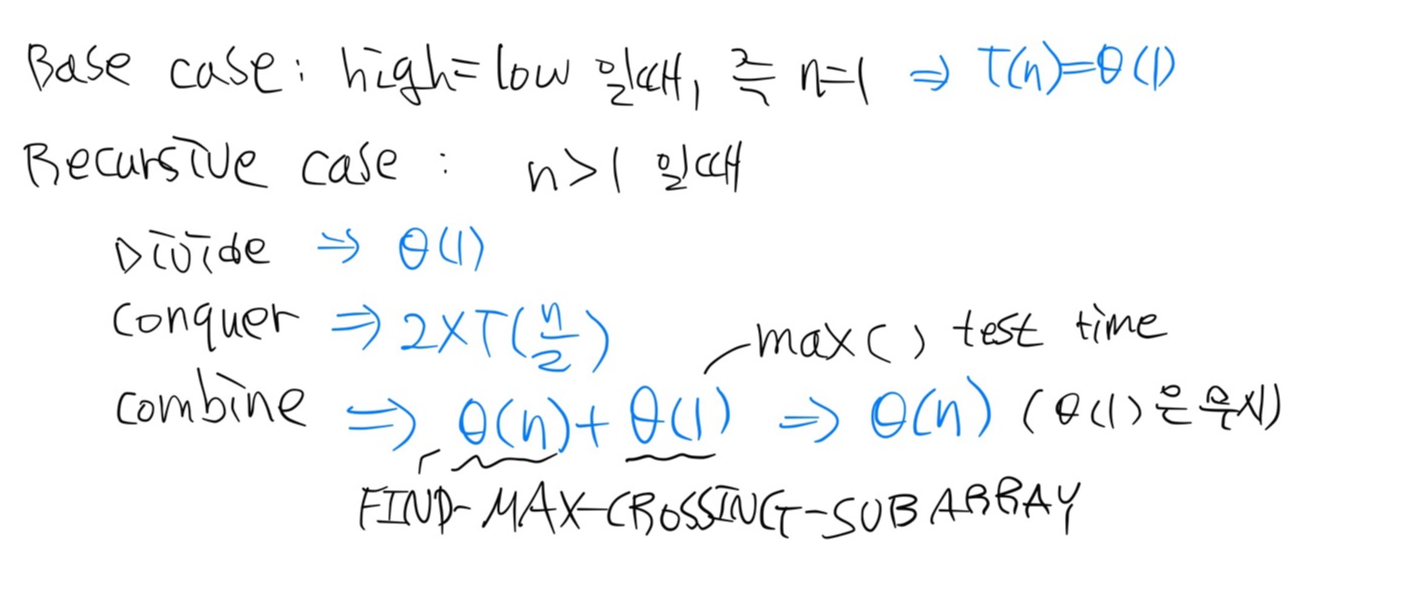

Master Method를 이용한 최종 T(n) 계산

Naive approach 와 Divide-and-conquer approach 로 도출한 값 비교
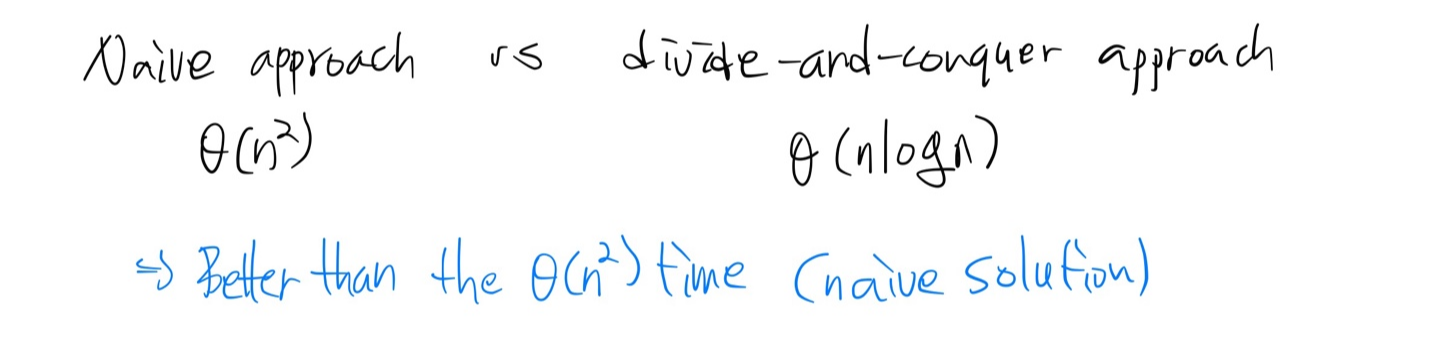
'Computer Science > algorithms' 카테고리의 다른 글
| [알고리즘] Quick sort: divide-and-conquer & loop invariants (0) | 2021.10.09 |
|---|---|
| [알고리즘] Maximum-subarray problem: 이해하기 (0) | 2021.10.09 |
| [알고리즘] Divide-and-Conquer algorithms & master method for solving recurrences (0) | 2021.10.07 |
| [알고리즘] Merge sort: divide-and-conquer & loop invariants (0) | 2021.10.07 |
| [알고리즘] Asymptotic Notation (0) | 2021.10.07 |
