(23.12.04)

가중치 매개변수의 기울기 구하는 방법
- 수치 미분: 단순하고, 구현하기 쉽다. but, 시간이 오래걸린다.
- back propagation: 효율적인 계산이 가능하다.
계산그래프
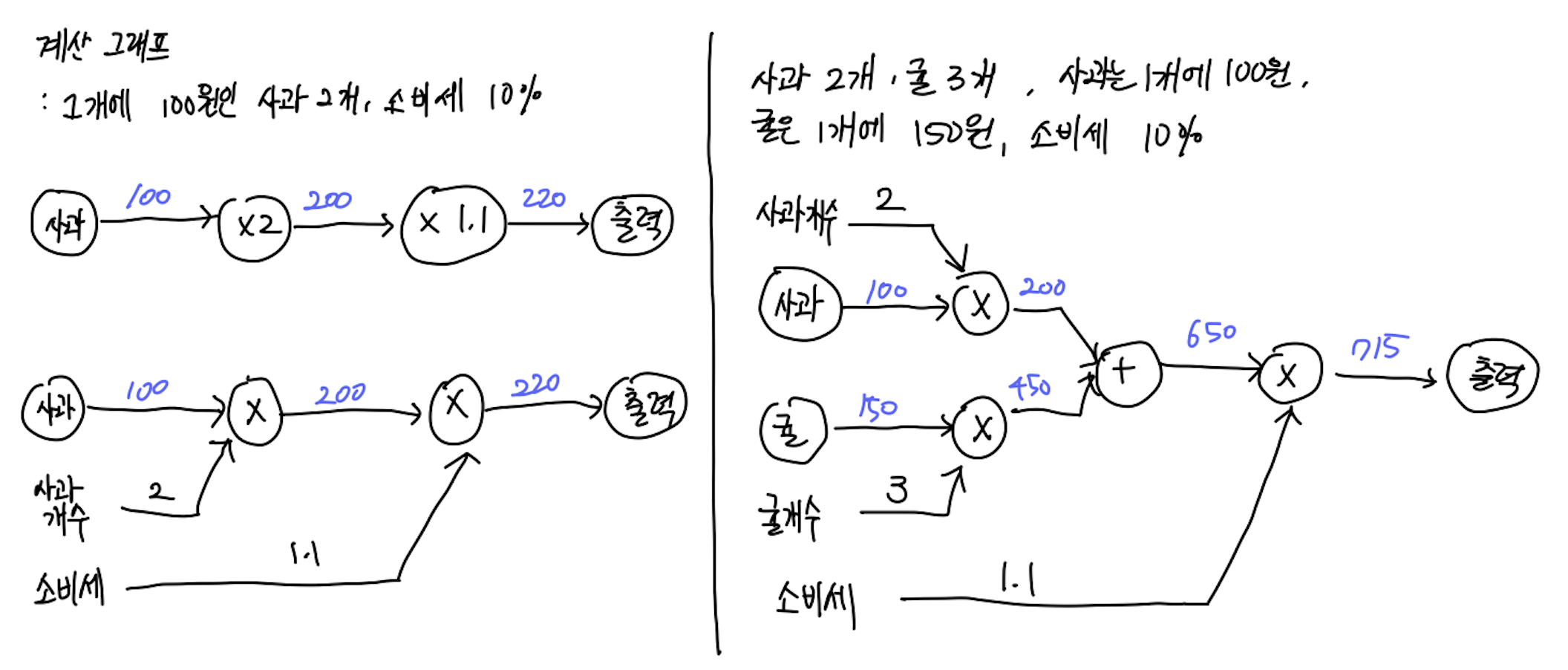
위와 같이 왼쪽에서 오른쪽으로 계산을 진행하는 것을 "순전파: forward propagation" 이라고 한다.
계산 그래프는 "국소적 계산"을 전파하여 최종결과를 낸다. (국소적 계산: 자신과 직접 관계된 작은 범위)
-> 아무리 복잡해도 각 노드에서는 단순한 계산이 이루어진다.
계산 그래프는 중간 계산 결과를 모두 저장할 수 있으며, 역전파를 통해 미분을 효율적으로 계산할 수 있다.
연쇄 법칙
: 합성 함수의 미분은 합성함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
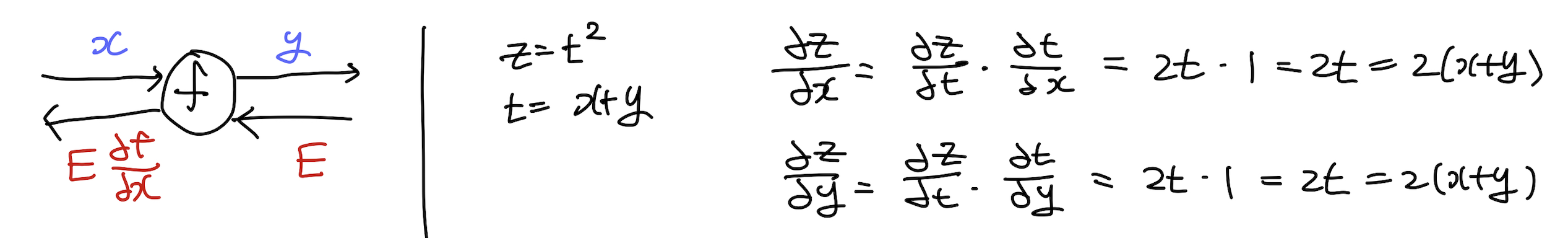

덧셈 노드의 역전파

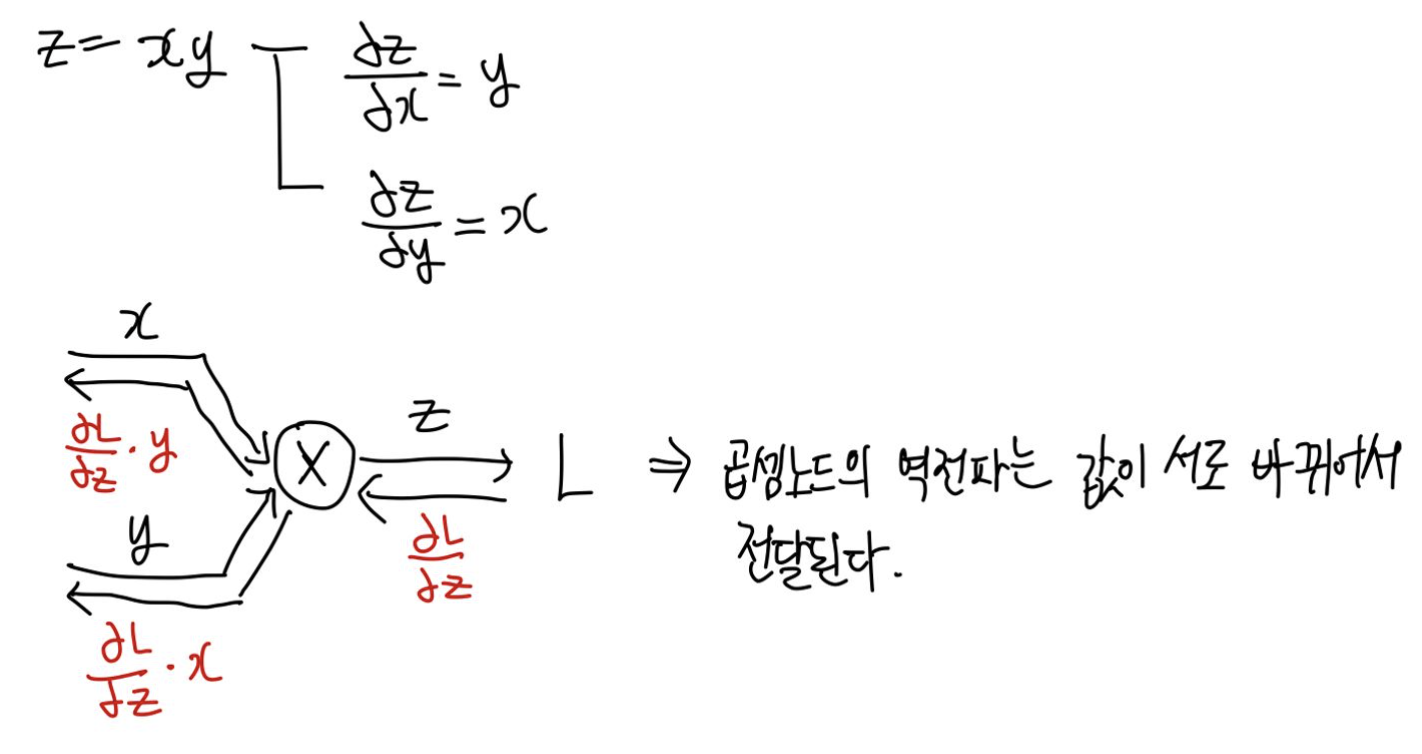
곱셈 노드의 역전파
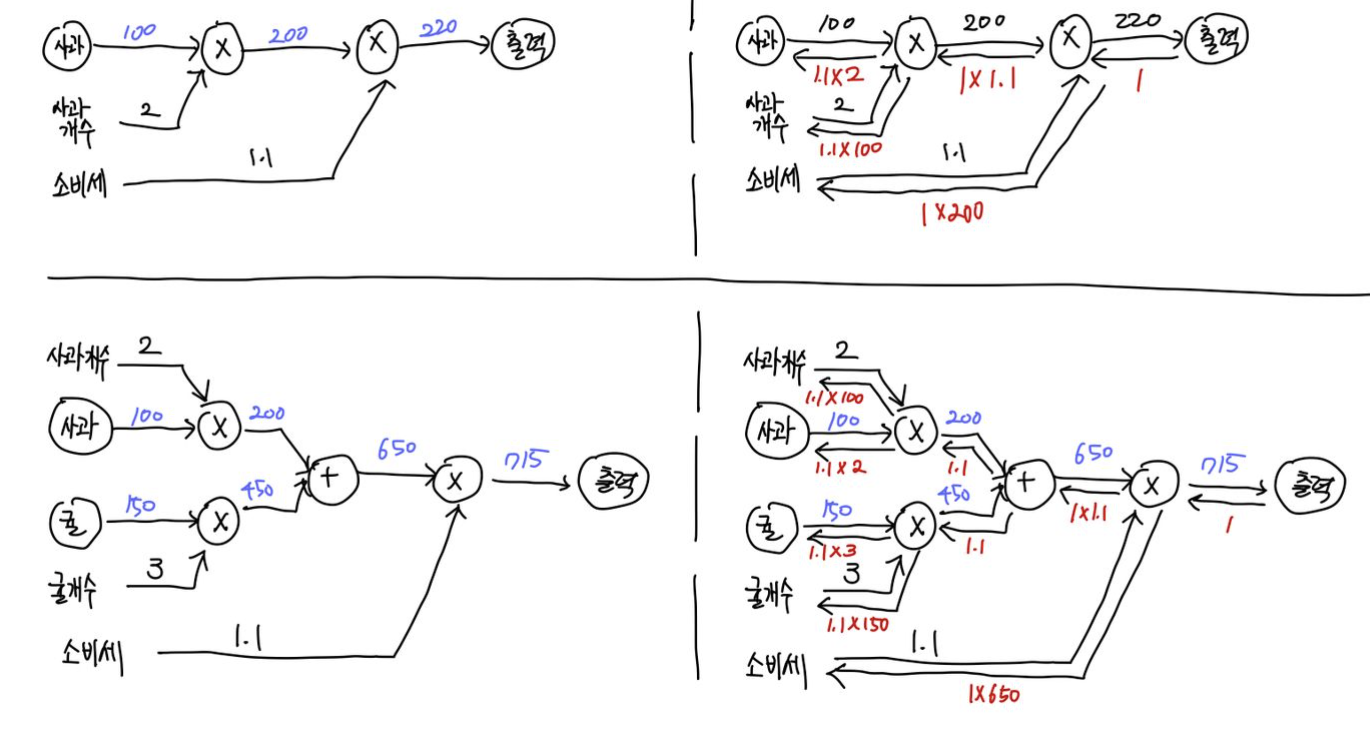
앞서 순전파로 나타냈던 계산그래프를 역전파를 포함하여 나타내면 아래와 같다.
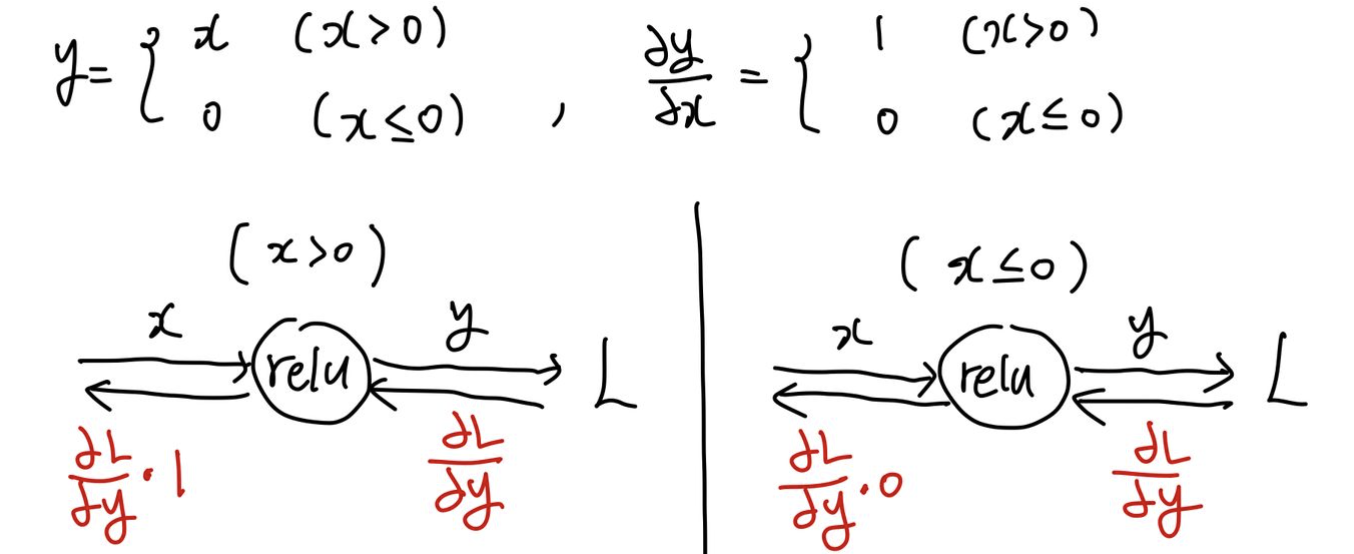
ReLU 계층의 역전파
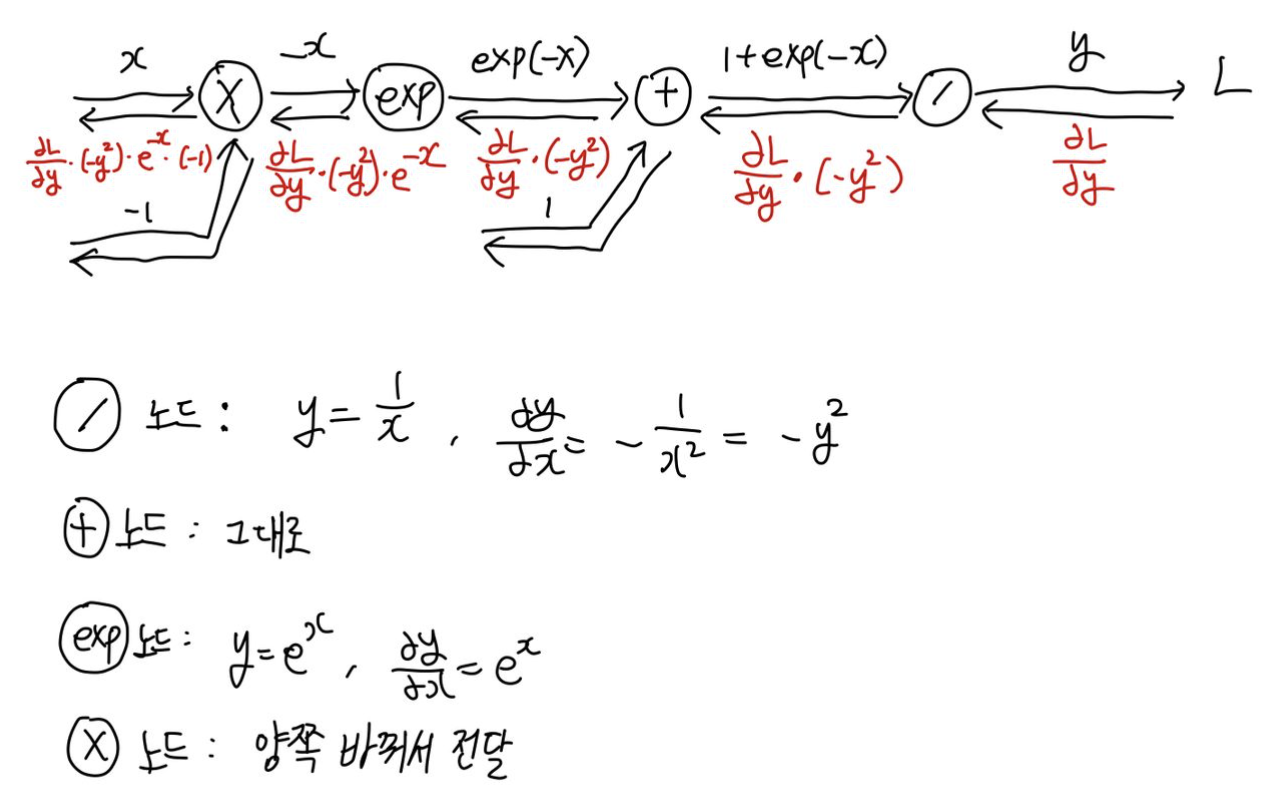
Sigmoid 계층의 역전파


Affine 계층의 역전파
Affine transformation: 순전파 때 수행하는 행렬의 곱


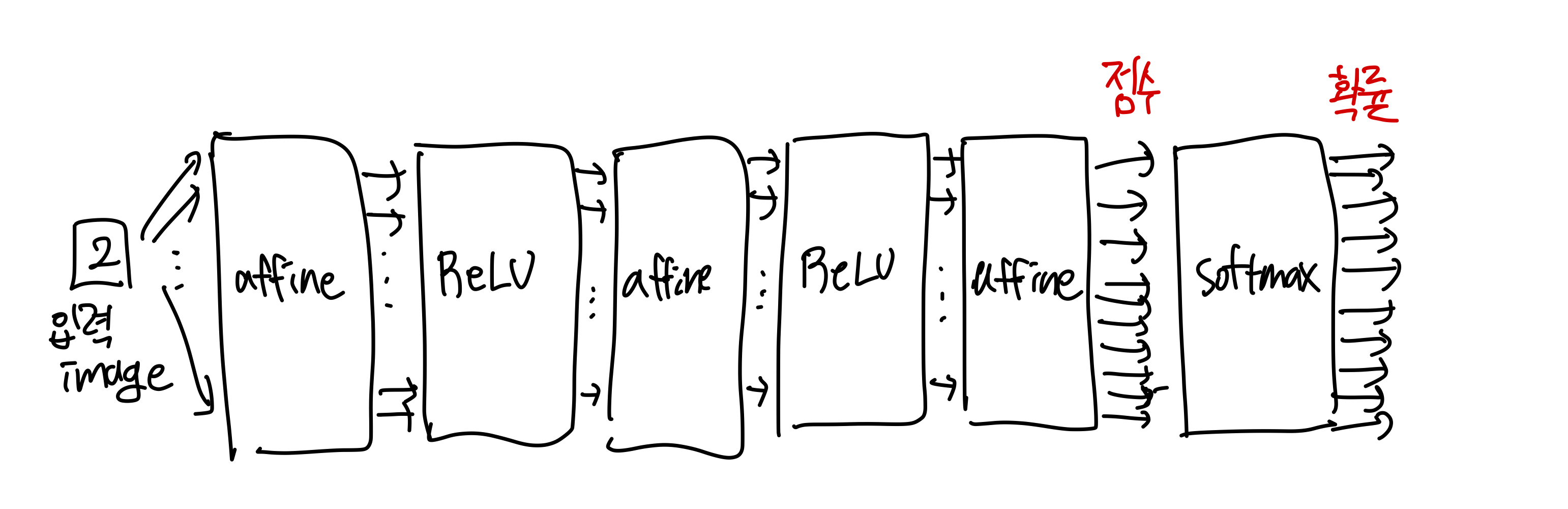
Softmax-with-loss 계층
- softmax 는 출력층에 사용되며, 입력값을 정규화한다.
- softmax 계층은 학습 시에만 필요하다.
728x90
'Computer Science > Deep Learning' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝 ch.7 CNN + ch.8 딥러닝 (1) | 2023.12.28 |
|---|---|
| 밑바닥부터 시작하는 딥러닝 ch.6 학습관련 기술들 (1) | 2023.12.28 |
| 밑바닥부터 시작하는 딥러닝 ch.4 신경망 학습 (0) | 2023.11.27 |
| 밑바닥부터 시작하는 딥러닝 ch.3 신경망 (2) | 2023.11.21 |
| 밑바닥부터 시작하는 딥러닝 ch.2 퍼셉트론 (0) | 2023.11.21 |
