(23.11.13)

퍼셉트론
- 프랑크 로젠블라트. 1975년 고안
- 신경망 (딥러닝) 의 기원이 되는 알고리즘
- 다수의 신호를 입력으로 받아 하나의 신호를 출력

-> y가 어떠한 임계값을 넘으면 1을 출력, 넘지 못하면 0을 출력
-> 가중치가 클수록, 해당 신호가 그만큼 중요하다는 것을 의미
논리회로
AND 게이트

NAND 게이트

OR 게이트

XOR 게이트
- 베타적 논리합
- x1, x2 중 하나만 1일 경우에만 1을 출력
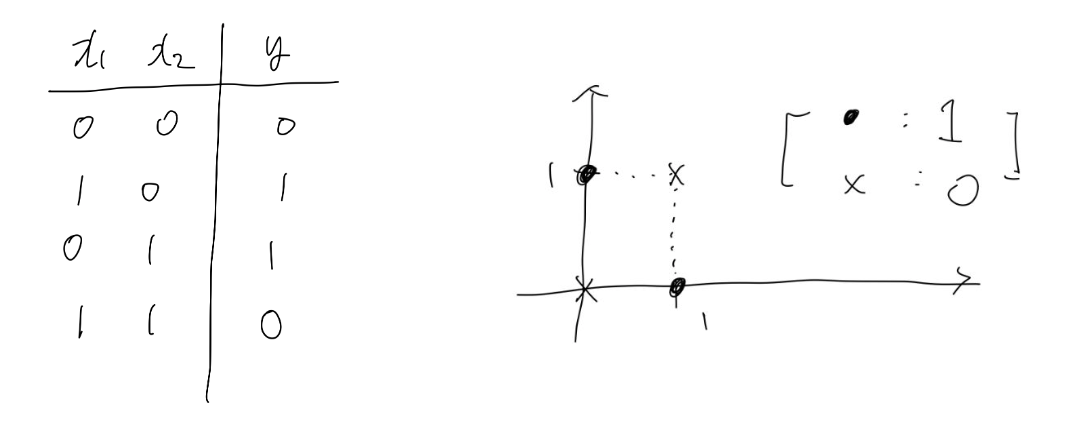
-> XOR 게이트의 입력과 출력을 좌표평면에 표현해보면, 어떠한 직선으로 영역으로 나눌 수 없다는 것을 알 수 있다.
====> 퍼셉트론의 한계 !!
AND, NAND, OR 게이트를 조합하여 XOR 게이트를 만들 수 있다.


-> AND, OR, NAND 는 단층 퍼셉트론
-> XOR 은 2층 퍼셉트론
python 코드 구현
# AND 게이트 구현
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.9
output = w1*x1 + w2*x2
if output > theta:
return 1
else:
return 0
# NAND 게이트 구현
def NAND(x1, x2):
w1, w2, theta = -0.5, -0.5, -0.9
output = w1*x1 + w2*x2
if output > theta:
return 1
else:
return 0

# threshold (theta) 를 bias (편향) 으로 바꾸어 구현
# AND 게이트 구현
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
output = np.sum(w*x) + b
if output > 0:
return 1
else:
return 0
# NAND 게이트 구현
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.9
output = np.sum(w*x) + b
if output > 0:
return 1
else:
return 0
# OR 게이트 구현
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.3
output = np.xum(w*x) + b
if output > 0:
return 1
else:
return 0
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
728x90
'Computer Science > Deep Learning' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝 ch.7 CNN + ch.8 딥러닝 (1) | 2023.12.28 |
|---|---|
| 밑바닥부터 시작하는 딥러닝 ch.6 학습관련 기술들 (1) | 2023.12.28 |
| 밑바닥부터 시작하는 딥러닝 ch.5 오차역전법 (0) | 2023.12.04 |
| 밑바닥부터 시작하는 딥러닝 ch.4 신경망 학습 (0) | 2023.11.27 |
| 밑바닥부터 시작하는 딥러닝 ch.3 신경망 (2) | 2023.11.21 |
