(23.11.27)

학습
- train data 로 부터 weight, bias (가중치 매개변수) 의 최적값을 얻는 것이다.
===> 신경망이 학습할 수 있도록 하는 지표를 loss function 이라고 한다.
- 학습의 목표: loss function의 결과값을 가장 작게 만드는 weight, bias 를 찾는 것
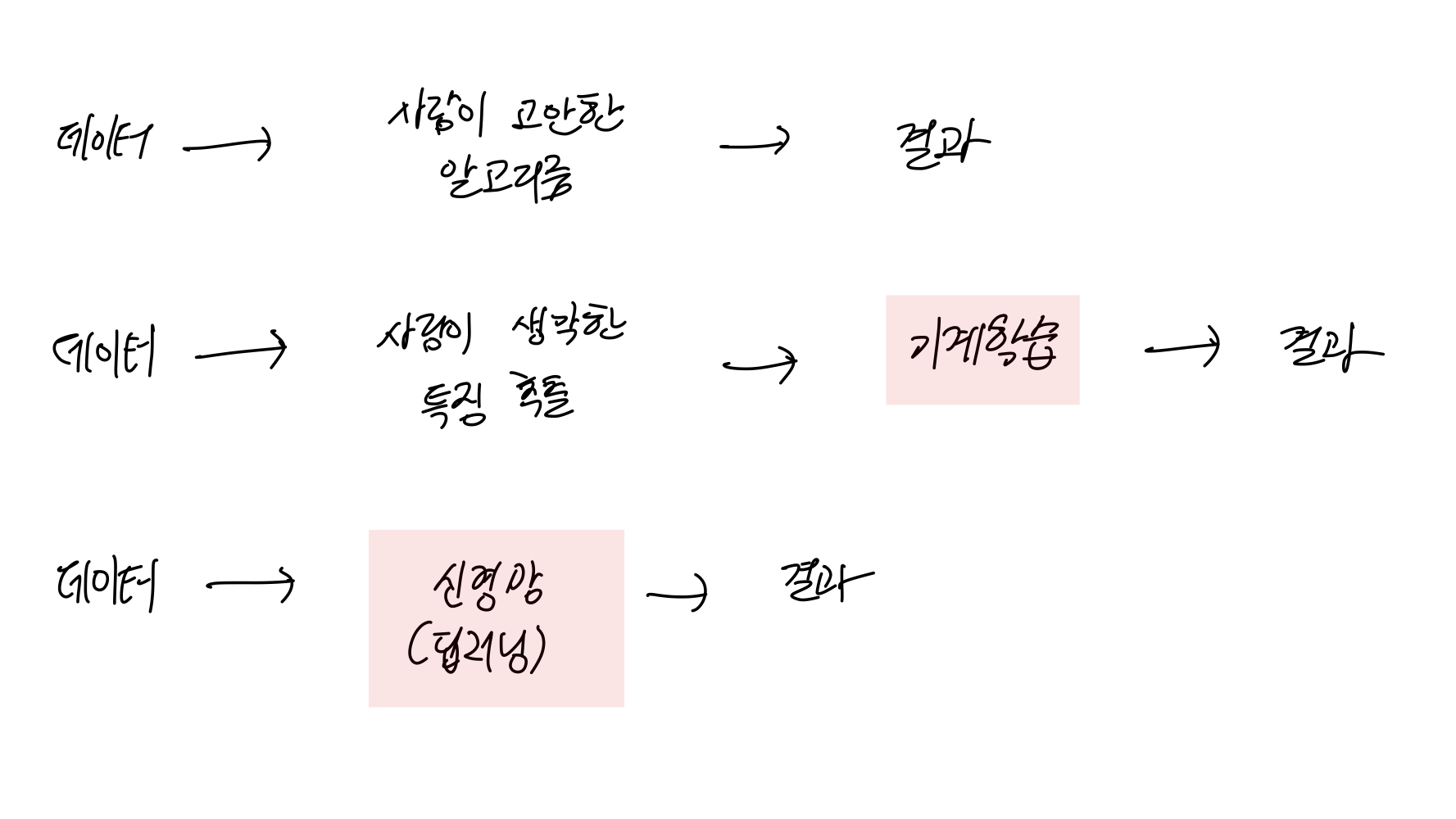
- 신경망은 end-to-end machine learning 이라고도 한다.
==> 입력부터 출력까지 사람의 개입이 없다는 의미.
데이터의 구분
: train + test
- train data 를 통해 학습하고, 최적의 weight, bias 를 찾는다.
- test data 를 통해 학습한 모델의 성능을 평가한다.
- 하나의 data 로 학습하고, 해당 data 로 평가하면, 그 성능은 당연히 높게 나온다.
==> 새로운 data 가 주어졌을 때에도 모델의 성능이 좋아야한다.
==> train data 에 대해서만 지나치게 최적화된 상태 : overfitting (과적합)
==> train data 에 대해서도 성능이 좋지 못한 상태 : underfitting (과소적합)
loss function
- 신경망 학습에서 loss function 은 학습 지표이다.
- loss function 의 값이 가장 작아지도록 하는 weight 와 bias 를 찾는다.
- 예시: 오차제곱합, 교차 엔트로피 오차



mini-batch 학습
- 전체 train data set 에서 일부분만 무작위로 골라서 학습할 때, 골라낸 data set을 mini-batch 라고 한다.
- 이 학습법을 mini-batch 학습이라고 한다.

- mini-batch 학습에 따른 loss function 수식

왜 학습지표로 손실함수를 설정하는가?
- 신경망을 학습할 때, loss function 의 값을 작게 하는 최적의 weight 와 bias 를 찾는다.
- loss function 의 기울기 (미분값) 를 계산해서 loss function 값이 최솟값을 갖도록 기울기의 반대 방향으로 향하게 weight와 bias 를 업데이트 한다.
===> 만약 기울기가 0이면, weight 와 bias 를 업데이트할 수 없게 된다.
- 정확도를 학습지표로 사용하지 않는 이유는 정확도의 기울기가 대부분 0 이기 때문이다.
- 마찬가지로 활성화 함수로 계단함수를 사용하지 않는 이유도 계단 함수의 대부분의 지점이 기울기가 0이기 때문에 weight와 bias 를 업데이트할 수 없기 때문이다.
미분과 경사하강법
- 미분: 어느 시점에서의 변화량
- 편미분: 변수가 여러 개인 함수에 대한 미분 -> 다른 변수는 상수로 취급하여 미분한다.

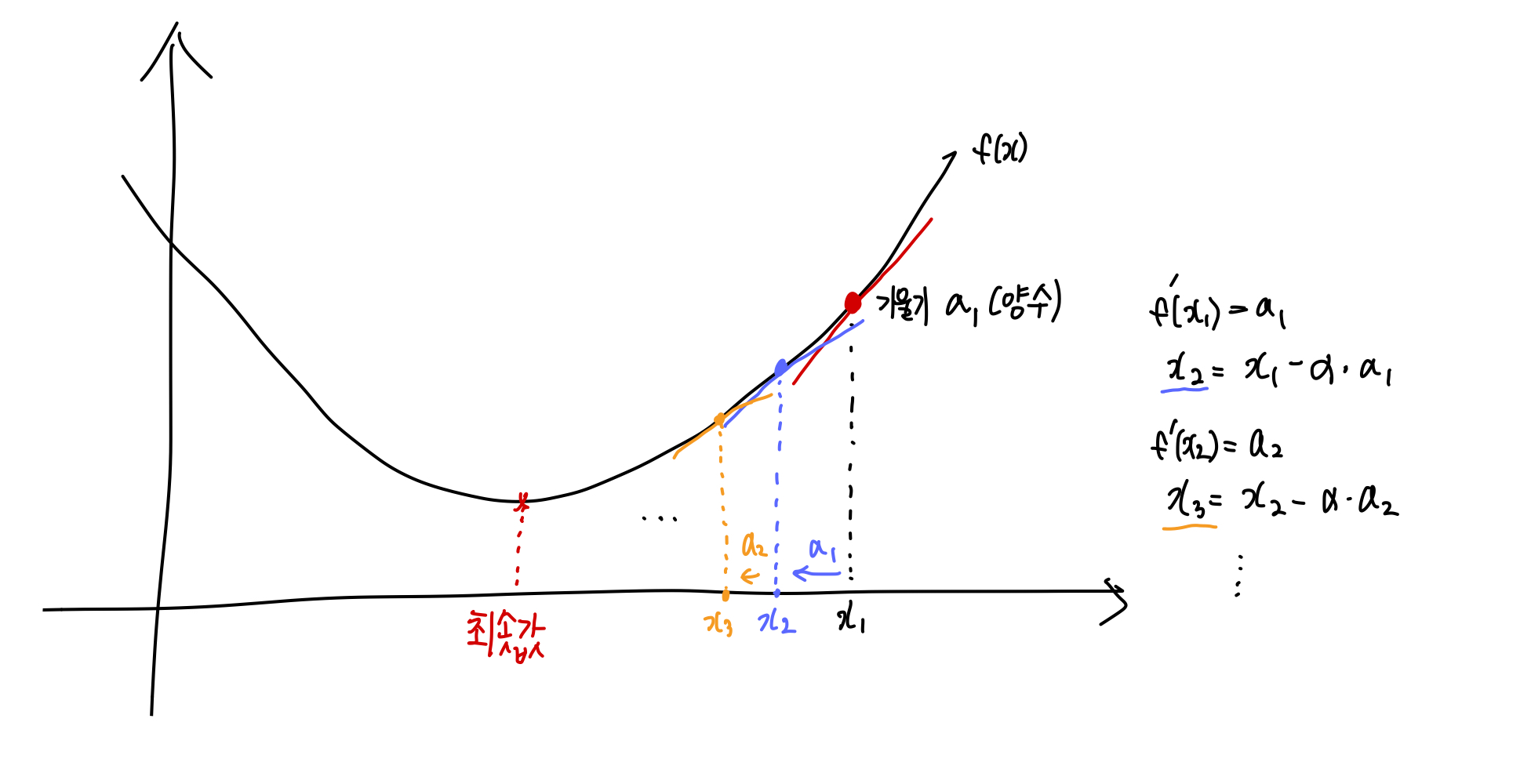
경사하강법 - gradient descent
- 기울기를 통해 function의 최솟값을 찾는 방법
- 신경망 (딥러닝) 분야에서는 기울기를 통해 loss function의 최솟값을 구하는 경사하강법을 사용하여 최적의 가중치 매개변수를 찾는다.
신경망에서의 기울기
- 가중치 매개변수 (weight, bias) 에 대한 loss function의 기울기
- 손실함수에 대한 모든 가중치 매개변수의 편미분을 벡터로 모아놓은 것
신경망 학습과정
1. train data 중에서 batch size 만큼만 무작위로 data 를 뽑는다. (mini-batch)
2. mini-batch 의 loss function 을 줄이기 위해 loss function 에 대한 weight, bias 의 기울기 (편미분) 를 구한다.
3. 구한 기울기를 바탕으로 loss function 값이 작아지는 방향으로 weight, bias 를 업데이트한다.
4. 1 ~ 3 단계를 반복한다.
===> 확률적으로 무작위로 골라낸 데이터에 대한 학습을 수행한다고 해서 확률적 경사 하강법 (stochastic gradient descent) 라고 부른다.
===> train data 50,000 개 중에서 100개의 mini-batch 를 골라 학습한다면, 1 epoch 은 50,000 / 100 = 500 회 이다.
'Computer Science > Deep Learning' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝 ch.7 CNN + ch.8 딥러닝 (1) | 2023.12.28 |
|---|---|
| 밑바닥부터 시작하는 딥러닝 ch.6 학습관련 기술들 (1) | 2023.12.28 |
| 밑바닥부터 시작하는 딥러닝 ch.5 오차역전법 (0) | 2023.12.04 |
| 밑바닥부터 시작하는 딥러닝 ch.3 신경망 (2) | 2023.11.21 |
| 밑바닥부터 시작하는 딥러닝 ch.2 퍼셉트론 (0) | 2023.11.21 |
