(2021.11.20)
이번에 정리할 부분 목차
11.1 메시지 무결성
11.1.1 문서와 핑거프린트
11.1.2 메시지와 메시지 다이제스트
11.1.3 차이점
11.1.4 무결성 확인
11.1.5 암호학적 해시 함수 기준
11.2 랜덤 오라클 모델
11.2.1 비둘기 집 원리
11.2.2 생일 문제
11.2.3 랜덤 오라클 모델에 대한 공격
11.2.4 구조에 대한 공격
11.3 메시지 인증
11.3.1 변경 탐지 코드
11.3.2 메시지 인증 코드
1. 11.1 메시지 무결성

무결성 점검(checking Integrity)
: 암호학적 해쉬함수를 이용해서 생성된 새로운 message digest와 그 이전의 message digest를 비교하여 message가 바뀌었는지 바뀌지않았는지를 확인할 수 있다.

암호학적 해쉬함수 기준

2. 11.2 랜덤 오라클 모델(Random Oracle Model)
> 암호학적 해시 함수의 이상적인 수학적인 모델
- 임의의 길이를 갖는 메시지에 대해서 0과 1로 이루어진 난수 스트링인 일정한 길이의 메시지 다이제스트 생성
- 기존에 생성된 메시지 다이제스트는 저장하여 동일한 메시지에 대해서 항상 동일한 메시지 다이제스트 제공
- 새로운 메시지에 대한 메시지 다이제스트 생성은 기존의 메시지 다이제스트 생성 결과와 독립적으로 랜덤하게 생성 (특정 공식이나 알고리즘 사용 불가)
- 메시지의 내용과는 상관없이 독립적이고 랜덤하게 메시지 다이제스트가 생성된다.
- 이상적인 방법이기는 하지만, 현실적으로 불가능하며 실용적이지 못하다. (모든 메시지에 대한 모든 메시지 다이제스트를 저장해두기 어렵기 때문)
11.2.1 비둘기 집 원리(Pigeonhole Principle)
> 만약 n+1 마리의 비둘기가 n개의 비둘기 집에 들어가있으면, 적어도 한 개의 비둘기 집에는 두 마리의 비둘기가 들어있다.
> 만약 kn+1 마리의 비둘기가 n개의 비둘기 집에 들어가있으면, 적어도 한 개의 비둘기 집에는 k+1 마리의 비둘기가 들어있다.

11.2.2 생일 문제
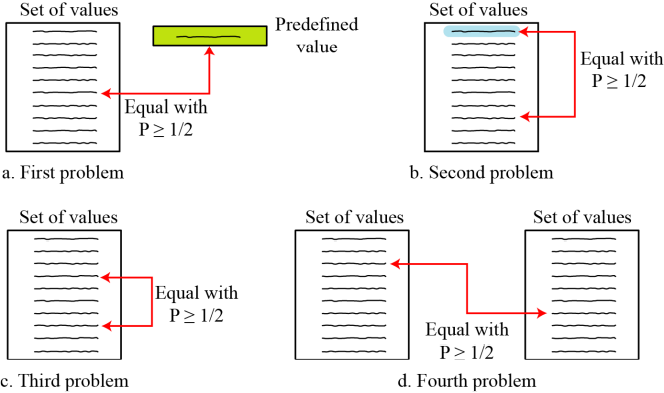
> 첫 번째 생일 문제
: 교실 안에 k 명의 학생이 있을 때, 적어도 한 학생이 특정 생일일 확률 P가 1/2보다 크거나 같으려면 k의 최솟값이 무엇인가?
> 두 번째 생일 문제
: 교실 안에 k명의 학생이 있을 때, 적어도 한 학생이 교사가 미리 선정한 학생과 같은 생일일 확률 P가 1/2보다 크거나 같으려며 k의 최솟값이 무엇인가?
> 세 번째 생일 문제
: 교실 안에 학생이 k명 있을 때, 적어도 두 학생이 같은 생일일 확률 P가 1/2보다 크거나 같으려면 k의 최솟값이 무엇인가?
> 네 번째 생일 문제
: 각 반에 학생이 k명씩 2개의 반이 있을 때, 적어도 첫 번째 반에서 선택된 한 학생과 다른 반에서 선택된 한 학생의 생일이 같을 확률 P가 1/2 이상이 되기 위해 필요한 k의 최솟값은 무엇인가?

11.2.3 랜덤 오라클 모델에 대한 공격
> 해쉬함수가 n 비트 메시지 다이제스트를 생성한다고 가정
> 메시지 다이제스트의 값이 0 ~ 2^n-1 사이에 균등하게 분포되는 확률변수라고 생각하면, 오라클은 매번 메시지에 대해서 이 값들 중 하나를 랜덤하게 선택
> 그러나 모든 값이 선택되는 것은 아님(어떤 값은 한 번도 선택되지 않을 수 있으며, 어떤 값은 여러번 선택될 수 있음)
> 해쉬함수 알고리즘이 공개되어 있고, 공격자는 메시지 다이제스트의 크기인 n값을 알고있다고 가정
1) 프리이미지공격(Preimage Attack)
y=h(M)이 주어지고, y=h(M')인 M'을 찾아야한다.

--> 첫 번째 생일 문제
--> 길이가 64비트인 메시지 다이제스트는 프리이미지 공격에 대해 안전하다.
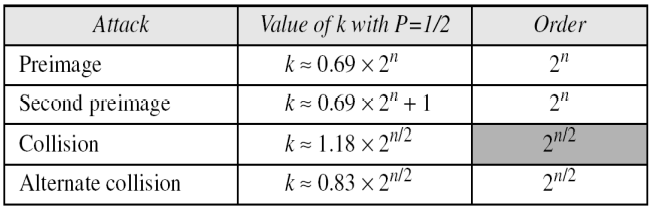
--> 프리이미지 공격의 어려움 정도는 2^n에 비례한다.
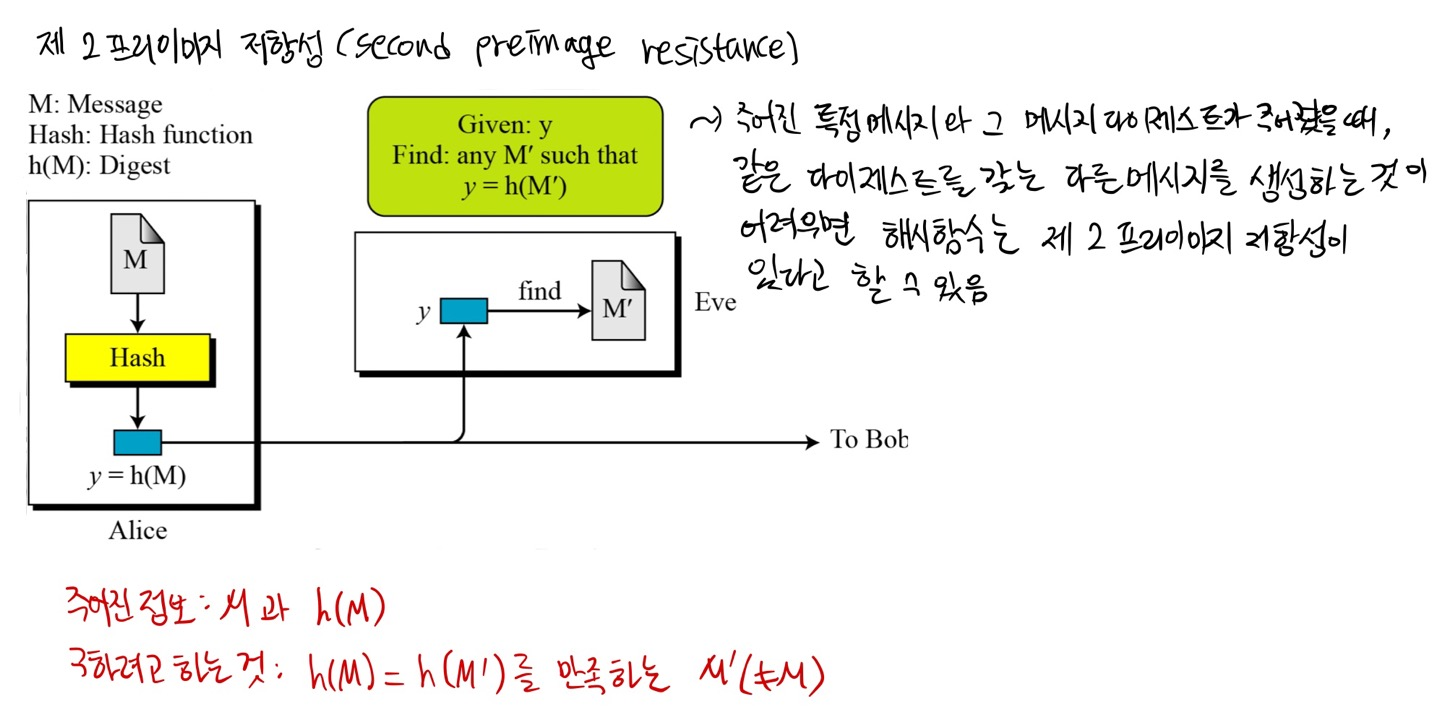
2) 제 2 프리이미지 공격(2nd Preimage Attack)
M과 h(M)이 주어지고, h(M)=h(M')인 서로 다른 M과 M'을 찾아야한다.

--> 두 번째 생일 문제
--> 제 2 프리이미지 공격의 어려움 정도는 2^n에 비례한다.
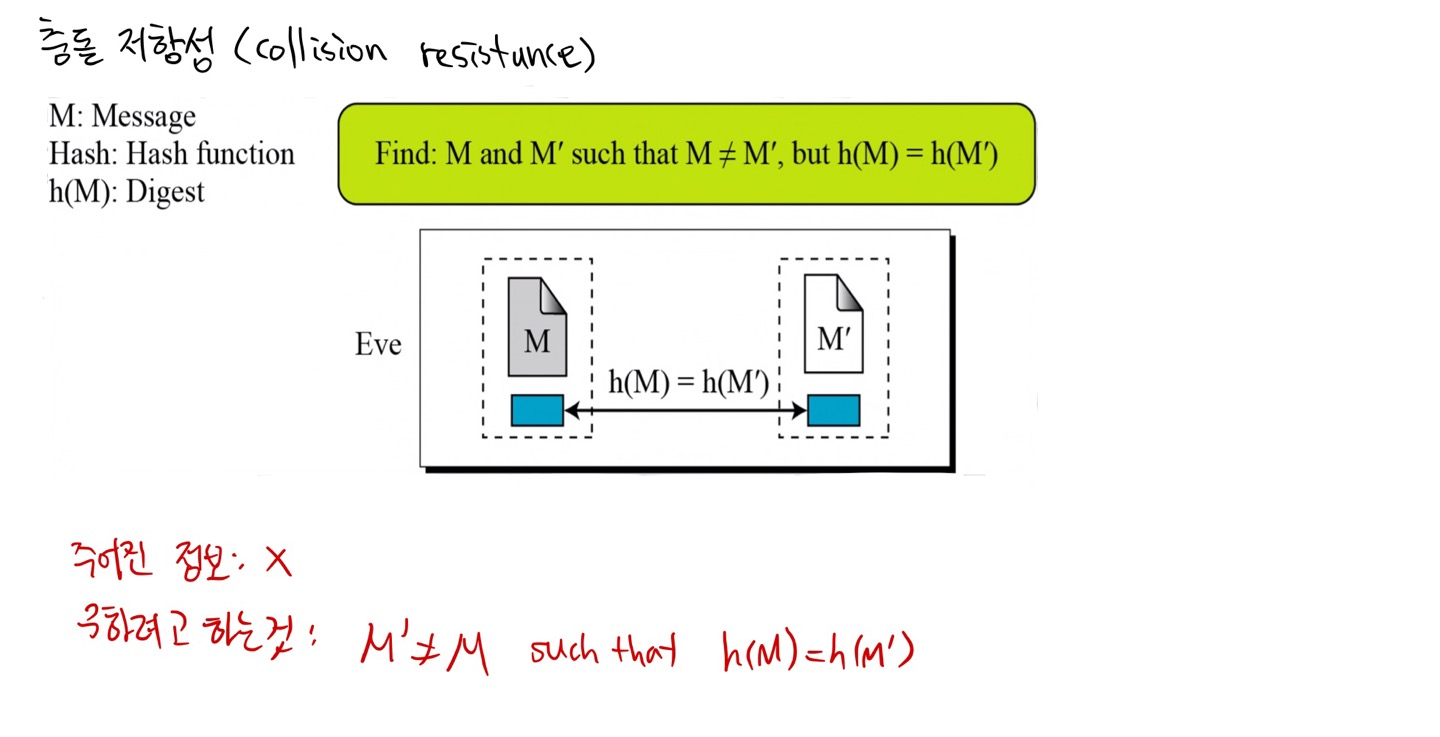
3) 충돌 공격(Collision Attack)
아무것도 주어지지 않고, h(M)=h(M')인 서로 다른 M과 M'을 찾아야한다.

--> 세 번째 생일 문제
-->충돌 공격의 어려움 정도는 2^(n/2)에 비례한다.
--> 길이가 64비트인 메시지 다이제스트는 충돌 공격에 대해 안전하지않다.
4) 또 다른 충돌 공격(Alternate Collision Attack)
아무것도 주어지지 않고, h(M)=h(M')인 서로 다른 M과 M'을 찾아야한다.

--> 네 번째 생일 문제
-->충돌 공격의 어려움 정도는 2^(1/2)에 비례한다.
> 최종 정리
3. 11.3 메시지 인증
11.3.1 변경 탐지 코드(MDC:modification detection code)
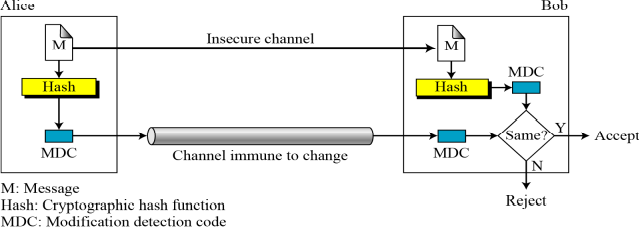
메시지의 무결성을 보장하는 메시지 다이제스트이다. --> 메시지가 변경되지 않았음을 증명해준다.
11.3.2 메시지 인증 코드(MAC:message authentication code)
> MAC
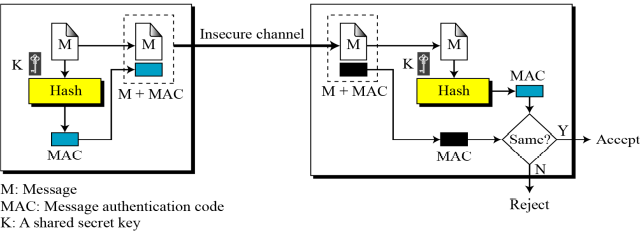
- Alice는 키와 메시지를 이어붙인 K|M에 해시함수를 적용하여 MAC인 h(K|M)을 생성한다.
- Alice는 메시지와 MAC을 안전하지 않은 채널을 통해 Bob에게 전송한다.
- Bob은 메시지와 MAC을 분리한 다음 K|M으로부터 새로운 MAC을 생성한다.
- Bob은 새로 생성한 MAC과 Alice로부터 받은 MAC을 비교한다.
- 같으면 해당 메시지는 인증된 것이고, 다르면 메시지는 변경된 것이다.
- 메시지 무결성과 데이터 송신자 인증을 동시에 보장한다.
- 비밀 키를 공유할 필요가 있으며, 별도의 안전한 채널 사용이 불필요하다.
- MAC의 안정성은 사용하는 해시 알고리즘의 안전성에 종속된다.
> 축소 MAC (nested MAC)
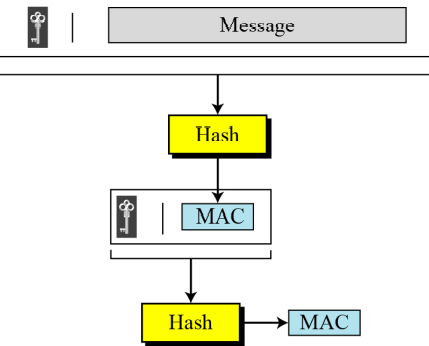
- 키와 메시지를 이어붙이고 hash하여 중간단계의 다이제스트를 생성한다.
- 키를 중간 단계 다이제스트에 이어붙이고 최종 다이제스트를 생성한다.
> HMAC (Hashed MAC)
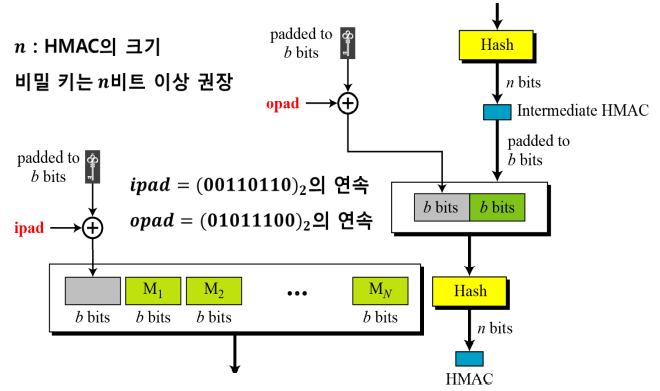
- 메시지를 길이가 b비트인 N개의 블록으로 나눈다.
- 비밀 키는 b-비트로 패딩해주고, ipad와 XOR연산을 하여 N개의 블록 맨 앞에 붙인다.
- 총 N+1개의 블록을 해시함수에 적용하여 n비트 다이제스트를 생성한다. 이를 중간 HMAC라고 부른다.
- n 비트로 된 중간 HMAC를 b-비트로 패딩해주고, opad와 XOR 연산을 하여 중간 HMAC를 b-비트로 패딩한 것 앞에 붙인다.
- 이를 해시함수에 적용하여 최종 n비트 HMAC를 생성한다.
(0으로 패딩함)
> CMAC (Cipher-based Message Authentication)
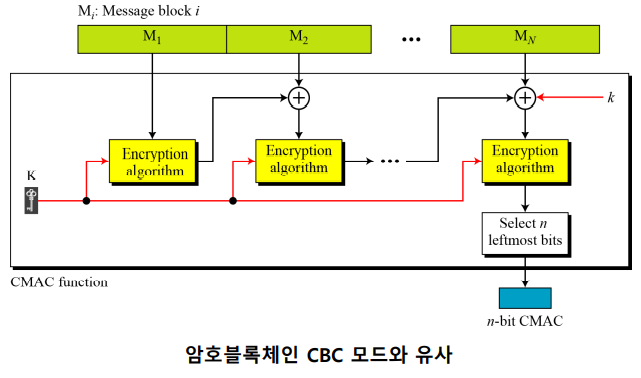
- 메시지를 N개의 블록으로 나눈다. 각 블록의 크기는 m비트이다. CMAC의 길이는 n비트이다.
- 마지막 블록이 m비트보다 작으면, 첫번째 비트는 1, 나머지 비트는 0으로 채워서 m비트로 패딩한다.
- 메시지의 첫번째 블록은 대칭키로 암호화하여 암호화된 m비트 블록을 생성한다.
- 이를 다음 메시지 블록과 XOR하여 대칭키로 암호화해서 m비트 블록을 생성한다.
- 이 과정을 반복하여 마지막 블록까지 암호화한다.
- 마지막 블록은 그 이전의 암호화된 m비트 블록과 새로운 키 k와 함께 패딩한 후, 대칭키로 암호화한다.
최종적인 m비트 블록에서 가장 왼쪽의 n비트만이 n비트 CMAC가 된다.
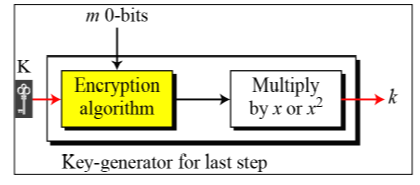
마지막 단계에서 마지막 메시지 블록이 패딩 될 경우와 그렇지 않을 경우에 따라 k가 결정된다.
패딩 될 경우: × (x^2)
패딩 되지 않을 경우: × (x)
(곱하기 연산은 GF(2^m)에서의 곱셈연산이다)
'Security > 현대 암호학' 카테고리의 다른 글
| [현대 암호학] 제 13장 - 디지털 서명 (0) | 2021.12.03 |
|---|---|
| [현대 암호학] 제 12장 - 암호학적 해시 함수 (0) | 2021.12.01 |
| [현대암호학] 제 10장 - 비대칭 키 암호 (0) | 2021.11.14 |
| [현대암호학] 제 9장 - 비대칭 키 암호수학 (2) (0) | 2021.11.14 |
| [현대암호학] 제 9장 - 비대칭 키 암호수학 (1) (0) | 2021.11.06 |

