(2021.11.07)
이번에 정리할 부분 목차
9.4 중국인의 나머지 정리
9.4.1 응용
9.5 2차 합동
9.5.1 모듈로가 소수인 2차 합동
9.5.2 모듈로가 합성수인 2차 합동 방정식 풀기
9.6 지수와 로그
9.6.1 지수
9.6.2 로그
9.4 중국인의 나머지 정리(CRT: Chinese remainder theorem)


9.5 2차 합동(quadratic congruence)

9.5.1 모듈로가 소수인 2차 합동



9.5.2 모듈로가 합성수인 2차 함동 방정식 풀기
모듈로가 합성수인 2차 합동 방정식은
모듈로가 소수인 2차 합동 방정식으로 분해해서 x에 대한 k쌍의 해를 구할 수 있다.
--> k쌍의 해로부터 2^k개의 연립방정식을 중국인의 나머지 정리를 이용해 풀면 x에 대한 2^k개의 해를 구할 수 있다.

모듈로가 합성수인 2차 합동 방정식의 해를 구하는 것의 복잡도는 합성수를 소인수분해하는 복잡도와 같다.


9.6 지수와 로그
9.6.1 지수
제곱-곱 방법
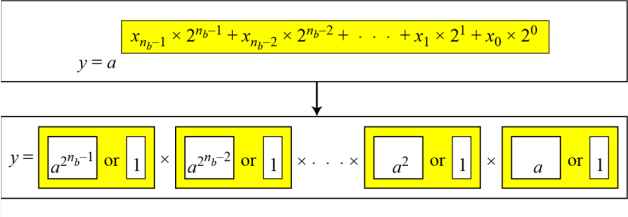
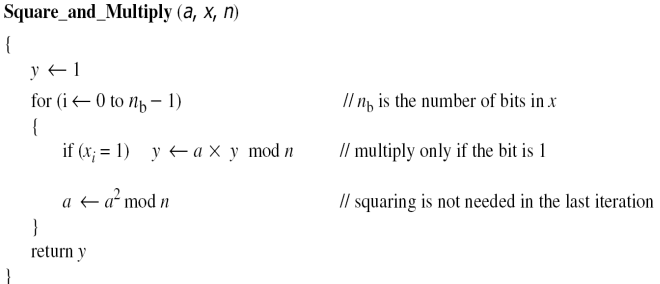
고속 지수 계산 알고리즘의 비트 연산 복잡도

9.6.2 로그




이산대수 로그를 계산하는 것의 복잡도는 합성수를 소인수분해하는 복잡도와 동일함
728x90
'Security > 현대 암호학' 카테고리의 다른 글
| [현대 암호학] 제 11장 - 메시지 무결성과 메시지 인증 (0) | 2021.11.21 |
|---|---|
| [현대암호학] 제 10장 - 비대칭 키 암호 (0) | 2021.11.14 |
| [현대암호학] 제 9장 - 비대칭 키 암호수학 (1) (0) | 2021.11.06 |
| [현대암호학] 제 8장 - 현대 대칭키 암호 (블록암호&스트림암호) (0) | 2021.11.01 |
| [현대암호학] 제 3장 - 고전 대칭키 암호 (전치암호&스트림암호&블록암호) (0) | 2021.11.01 |
