(2021.11.14)
이번에 정리할 부분 목차
10.1 대칭 키 암호 시스템과 비대칭 키 암호시스템의 차이점
10.1.1 키
10.1.2 일반적인 아이디어
10.1.3 양쪽에 필요한 것
10.1.4 트랩도어 일방향 함수
10.1.5 배낭 암호
10.2 RSA 암호시스템
10.2.1 개요
10.2.2 절차
10.2.3 간단한 예제
10.2.4 RSA에 대한 공격
10.2.5 권장 사항
10.2.6 최적 비대칭 암호 패딩(OAEP)
10.3 Rabin 암호 시스템
10.3.1 절차
10.3.2 Rabin 시스템의 보안성
10.4 EIGamal 암호시스템
10.4.1 EIGamal 암호시스템
10.4.2 절차
10.4.3 키 생성
10.4.4 EIGamal의 보안성
10.5 타원 곡선 암호 시스템 (교수님이 설명 생략하셨음)
RSA에 대한 공격, 최적 비대칭 암호패딩, RABIN, EIGamal 은 교수님이 자세하게 다루시지는 않으셨다.
1. 10.1 대칭 키 암호 시스템과 비대칭 키 암호 시스템의 차이점
대칭 키/비대칭 키 암호 시스템은 서로 상호보완적이다.
- n명의 그룹에 필요한 대칭키는 n(n-1)/2 개의 키가 필요하지만, 비대칭 키는 n개의 개별적인 키가 필요하다.
- 대칭 키 암호시스템은 비밀을 공유하는 것에, 비대칭 키 암호시스템은 개별적 비밀에 기반을 두고 있다.
- 대칭 키 암호시스템은 기호를 대체시키거나 치환하는 것이고, 비대칭 키 암호시스템은 수를 다른 수로 변경하는 것이다.
10.1.1 키
비대칭 키: 공개 키(public key)와 개인 키(private key)
대칭 키: 비밀 키(secret key)

> 암호 시스템의 비 대칭성: 쌍방간의 각자 공개키, 개인키 사용
> 수신자의 책임: 키 생성, 키 배포, 무결성과 인증 제공
> 평문(plaintext)이나 암호문(ciphertext)이 정수로 다루어진다.

1.0.1. 트랩도어 일방향 함수
> 함수(function)
> 일방향 함수(one-way function)
-- 주어진 x에 대하여 y=f(x)는 계산이 쉽다.
-- 주어진 y에 대하여 x=f-1(y) 게산이 쉽다.
> 트랩도어 일방향 함수(trapdoor one-way function)
-- y와 트랩도어(비밀)가 주어지면, x=f-1(y) 계산이 쉽다.
예제)
n이 매우 큰 수라면, n=pxq는 일방향 함수이다.
: 주어진 p와 q로부터 n을 계산하는 것은 매우 쉽지만, 주어진 n으로부터 p와 q를 계산하는 것은 매우 어렵다. 이 문제가 소인수분해 문제이다.
n이 매우 큰 수라면, 함수 y=x^k mod n은 트랩도어 일방향 함수이다.
: 주어진 x, k, n에 대해 y를 계산하는 것은 쉽지만, y, k, n가 주어졌을 떄, x를 계산해내는 것은 매우 어렵다. 이 문제가 모듈로 지수/로그 계산 문제이다.
--> k x k' = 1 mod φ(n) 이 되는 트랩도어 k' 을 알고 있다면, x=y^(k') mod n 을 이용해서 x를 구할 수 있다.
10.1.5 배낭 암호(knapsack cryptosystem)
a=[a1,a2, ,,, ,ak], x=[x1,x2, ,,, ,xk], xi=0 또는 1
s=knapsackSum(a,x)=x1a1+x2a2+ ,,, + xkak
주어진 a와 x로부터 s를 계산하는 것은 쉽지만, s와 a가 주어졌을 때 x를 구하는 것은 어렵다.
---> knapsackSum(a,x)는 일방향 함수이다.
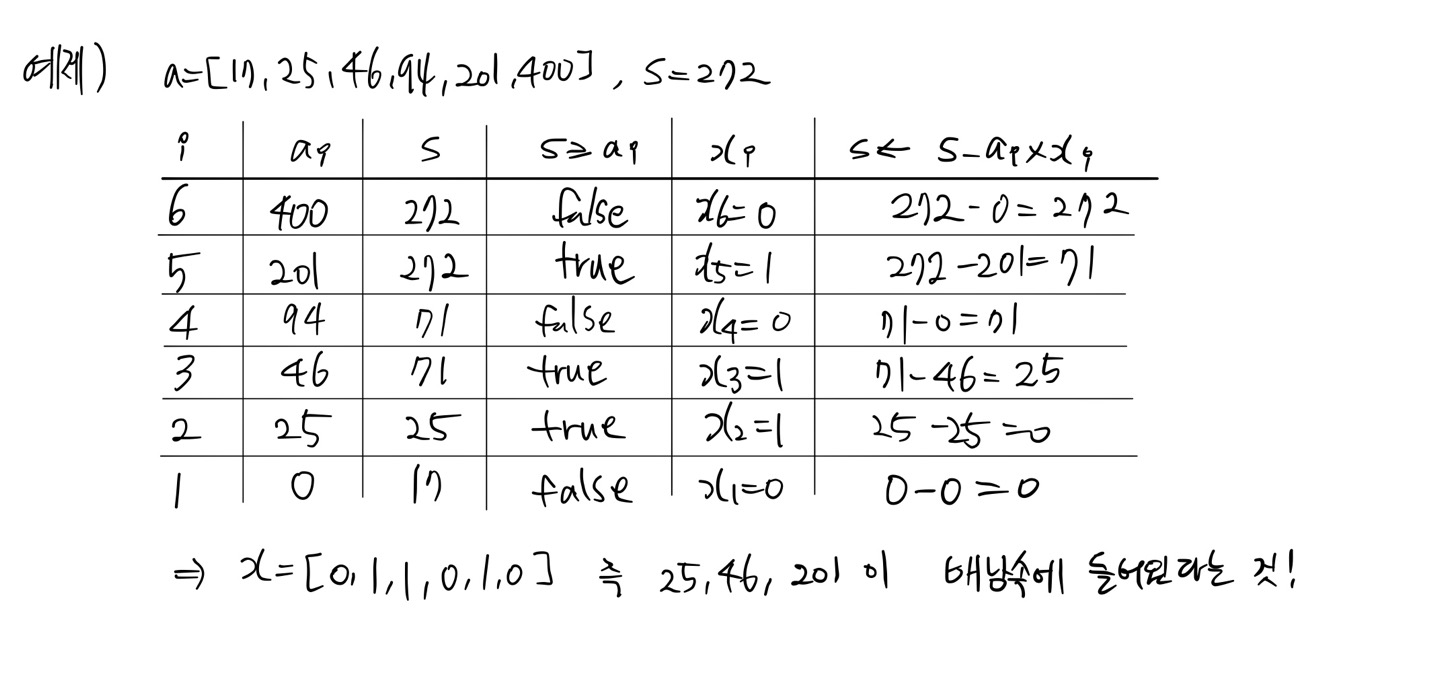
초증가 순서짝(superincreasing tuple): ai ≥ a1 + a2 + ... + ai-1
주어진 a가 초증가 순서짝이면, s와 a가 주어진다면, x를 구하는 것은 쉽다.
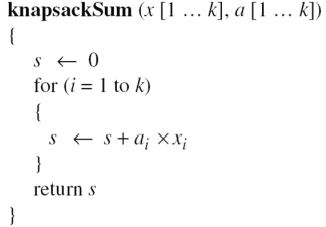
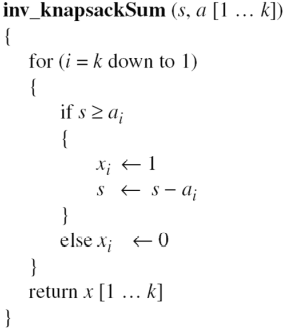
1.0.2. 배낭 암호를 이용한 비밀 통신
키 생성
1. 초증가 순서짝 b=[b1, b2, ... , bk]를 만든다.
2. 모듈로 n>b1+b2+ ... +bk 을 선정한다.
3. n과 서로소이면서 1≤r≤n-1 인 임의의 정수 r을 선택한다.
4. ti=r x bi mod n 을 만족하는 순서짝 t=[t1, t2, ... ,tk] 를 만든다.
5. 치환을 통해 새로운 순서짝 a=[a1, a2, ... , ak] 을 구한다.
6. a는 공개키로 n, r, b 는 개인키로 사용한다.
암호화
1. 자신의 메시지를 순서짝 x=[x1,x2, ... , xk] 로 변환시킨다. 여기에서 xi=0 or 1이며, 순서짝 x가 평문이다.
2. 주어진 공개키 즉, 순서짝 a=[a1,a2, ..., ak] 를 이용하여 s=knapsackSum(a,x)을 계산하면, s가 암호문이다.
복호화
1. 보관 중인 개인키 즉, n,r 을 이용하여 암호문 s로부터 s'=s x r-1 mod n 을 계산한다.
2. 보관 중인 개인키 즉, 순서짝 b=[b1,b2, ..., bk]를 이용하여 x'- inv_knapsackSum(s',b) 을 계산하여 x'을 구한다.
3. x' 을 치환하면 x가 평문이다.



2. 10.2 RSA 암호시스템
모듈로 n과 지수 e는 공개키, 지수 d는 개인키로 사용한다.
RSA는 모듈로 지수계산을 이용해서 암호화/복호화 한다. --> 이를 공격하려면 이브는 C^(e/1)mod n을 계산해야한다.
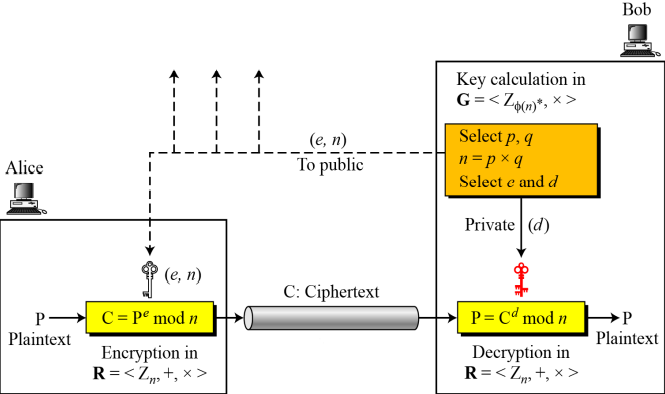
암호화/복호화: 환(Ring)
R=<Zn,+,×>
모듈로 n이 공개되어 있으므로 누구나 이 환을 이용해서 메시지를 암호화해서 보낼 수 있다.
키생성: 군(Group)
G=<Zφ(n)*,×>n=p×q를 만족하는 p와 q, 모듈로 φ(n)을 비밀로 하여, 공개키와 개인키를 생성하는 데에 사용한다.


RSA에 대한 공격(attack on RSA)
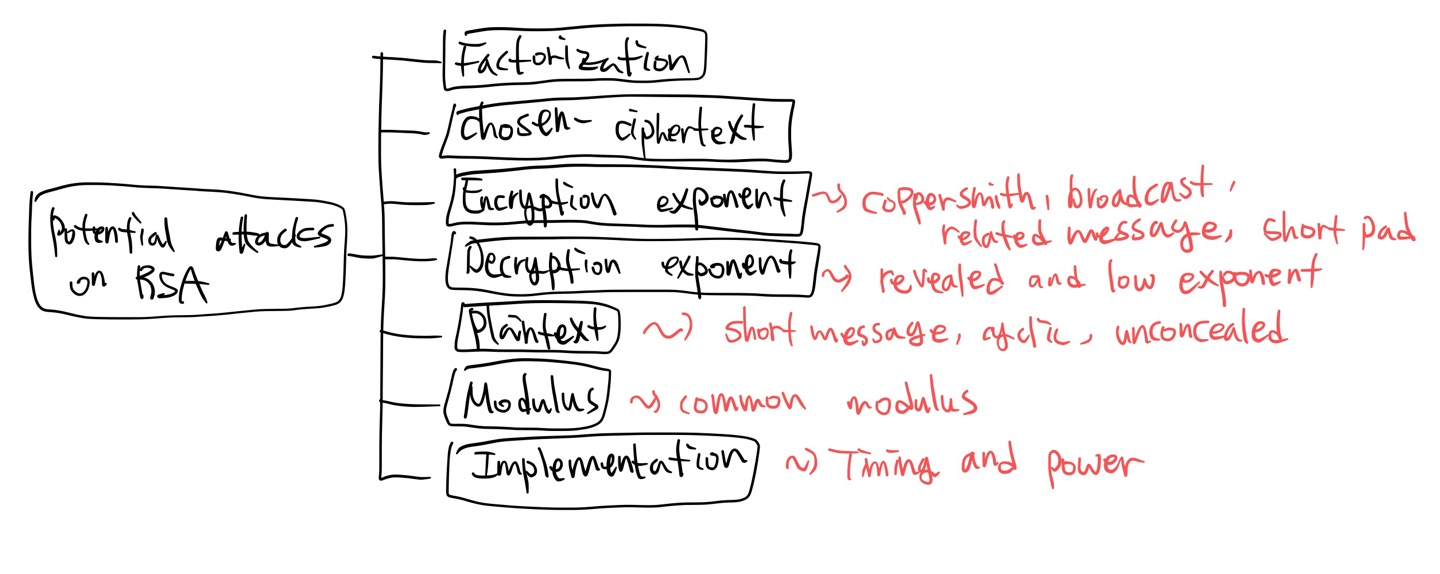
1) 소인수분해 공격
: 공개된 모듈로 n을 소인수분해하여 n = p x q 을 만족하는 p와 q, 모듈로 φ(n)을 구한 다음 지수 e의 역원인 지수 d를 알아내는 공격
2) 선택 암호문 공격
: 암호문 C을 중간에 가로채어 임의의 수 X를 선정하여 C x X^e mod n 를 보내 복호화한 결과 Z를 얻어내어 P= Z x X^-1 mod n 을 알아내는 공격
3) 암호화 지수에 대한 공격
: 암호화 시간 단축을 위해서 암호화 지수 e의 값을 지나치게 작게 선정하는 경우에 대한 공격
: coppersmith, broadcast, related message, short pad 4가지 종류의 공격이 있다.
4) 복호화 지수에 대한 공격
: 복호화 시간 단축을 위해서 복호화 지수 d의 값을 너무 작게 선정하거나 복호화 지수 d의 값이 노출된 상태에서 계속해서 동일한 모듈로 n을 사용하는 경우에 대한 공격
: revealed and low exponent 2가지 종류의 공격이 있다.
5) 평문 공격
: 전화번호 같이 길이가 짧은 평문에 대한 전수 조사, 암호문을 계속 암호화하면 언젠가 평문이 된다는 것을 이용한 공격
: short message, cyclic, unconcealed 3가지 종류의 공격
6) 모듈로에 대한 공격
: 특정 집단이 동일한 모듈로 n을 사용하는 경우에 대한 공격
RSA에서 짧은 메시지는 짧은 메시지 공격으로 암호문을 위험에 빠뜨리게 할 수 있다. 아무 의미없는 데이터/메시지를 붙여서 (padding) Eve의 공격 작업을 어렵게 할 수 있지만, Eve가 충분히 다시 공격할 수 있다.--> 이에 대한 해결책으로 최적 비대칭 암호 패딩(OAEP)라는 절차를 적용할 수 있다.OAEP는 전송 중에 한비트라도 오류가 발생하면 RSA는 실패하게 된다.
3. 10.3 Rabin 암호시스템
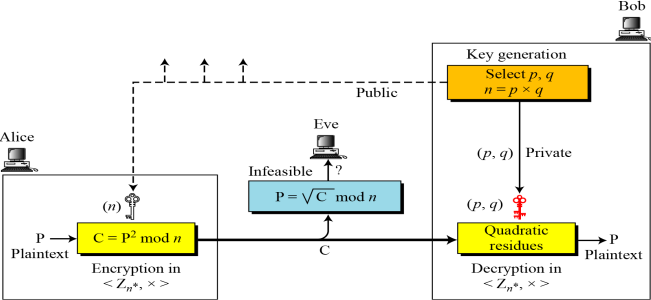
Rabin 암호시스템은 e와 d의 값이 고정된 RSA 암호시스템이다.
공개키는 n, 개인키는 순서쌍 (p,q)이다.
누구나 n을 이용해서 암호화할 수 있으나, 오직 Bob만 p,q를 이용해서 복호화할 수 있다.
Bob이 RSA를 사용한다면, Bob은 d와 n을 간직하고 키를 생성한 다음 p와 q와 φ(n)은 버린다.
Bob이 Rabin을 사용한다면, Bob은 p와 q값을 계속 가지고 있어야한다.
4. 10.4 EIGamal 암호시스템
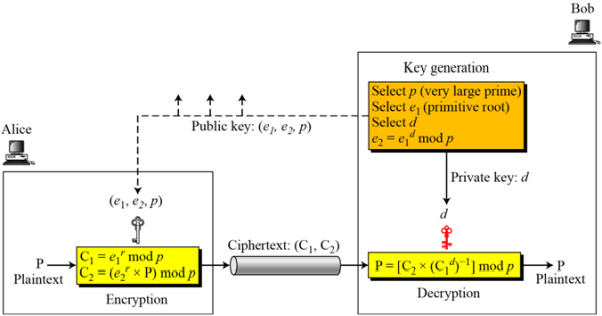
ㅇㅇ
Alice가 r을 생성한 후에 비밀로 유지한다는 점이 흥미롭다.
Bob은 d를 생성하고 비밀로 유지한다.
EIGamal 암호시스템의 암호화와 복호화의 비트-연산 복잡도는 다항식 수준이다.
'Security > 현대 암호학' 카테고리의 다른 글
| [현대 암호학] 제 12장 - 암호학적 해시 함수 (0) | 2021.12.01 |
|---|---|
| [현대 암호학] 제 11장 - 메시지 무결성과 메시지 인증 (0) | 2021.11.21 |
| [현대암호학] 제 9장 - 비대칭 키 암호수학 (2) (0) | 2021.11.14 |
| [현대암호학] 제 9장 - 비대칭 키 암호수학 (1) (0) | 2021.11.06 |
| [현대암호학] 제 8장 - 현대 대칭키 암호 (블록암호&스트림암호) (0) | 2021.11.01 |
