(2021.11.17)
알고리즘 수업들으면서 정리하기 20탄
w11-2 녹화강의, w12-1 실강
minimum spanning tree와 prim algorithm 내용이다.
Minimum Spanninng Tree
최소 신장 트리 --> 줄여서 MST
input: 방향성 없는 연결 그래프 connected, undirected graph G=(V,E) (각 edge 들에 weigth가 있음)
output: acyclic subset T of the edges of G (G의 모서리들의 cycle 없는 subset)
- Model은 undirected graph G=(V,E) 임
- 각 edge (u,v) ∈ E 에는 weight w(u,v) 가 있음 (u,v ⊂ V)
- acyclic T⊆E 에 대해서 모든 노드들은 연결되어있음
- acyclic T⊆E 에 대해서 weight w(u,v)∈T 의 합은 minimized 임.
- T는 acyclic이고, 모든 vertex와 연결되어있기 떄문에 tree를 형성한다고 할 수 있음
- cylce이 없도록 하려면 T의 edge 개수는 (vertex의 수 - 1) 이어야함.
ㅇ
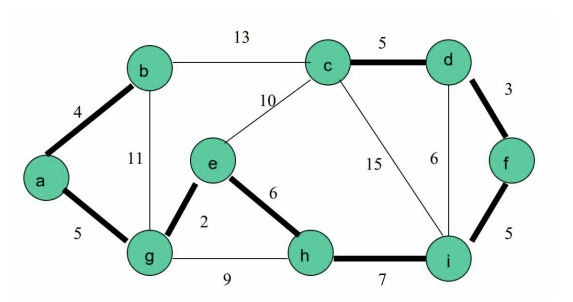
1) 노드들은 모두 연결되어있어야 하며
2) cycle을 만들면 안되고
3) cost는 최소가 되어야한다.
위의 그림에서 solution = { (b,a), (a,g), (g,e), (e,h), (h,i), (i,f), (f,d), (d,c) }
방향성이 없는 그래프이기 때문에 (b,a)와 (a,b) 는 같은 의미를 가진다.
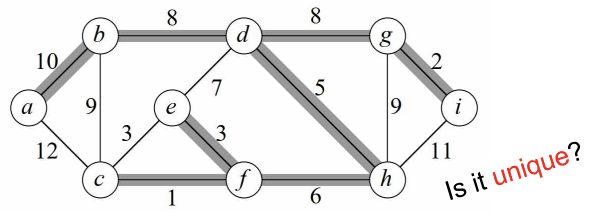
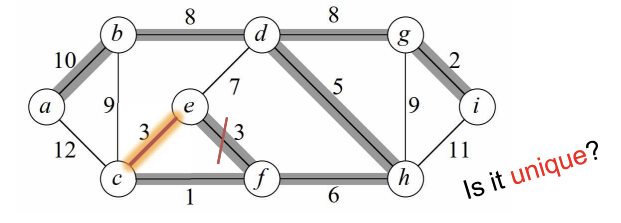
위의 두 그림을 보면, 같은 최소 cost를 가지는 데 두가지의 방법이 있기 때문에 위 그림의 solution은 unique 하다고 말할 수 없다.
MST problem을 해결하는 두가지의 알고리즘이 있다
- Kruskal's algorithm
- Prim's algorithm
그리고 greedy 전략이 이용된다.
greedy 전략은 generic method에서 비롯되었다.
Kruskal 알고리즘과 prim 알고리즘은 generic MST 알고리즘을 강화한 알고리즘이다.
먼저 Generic MST algorithm에 대해서 정리해보자.

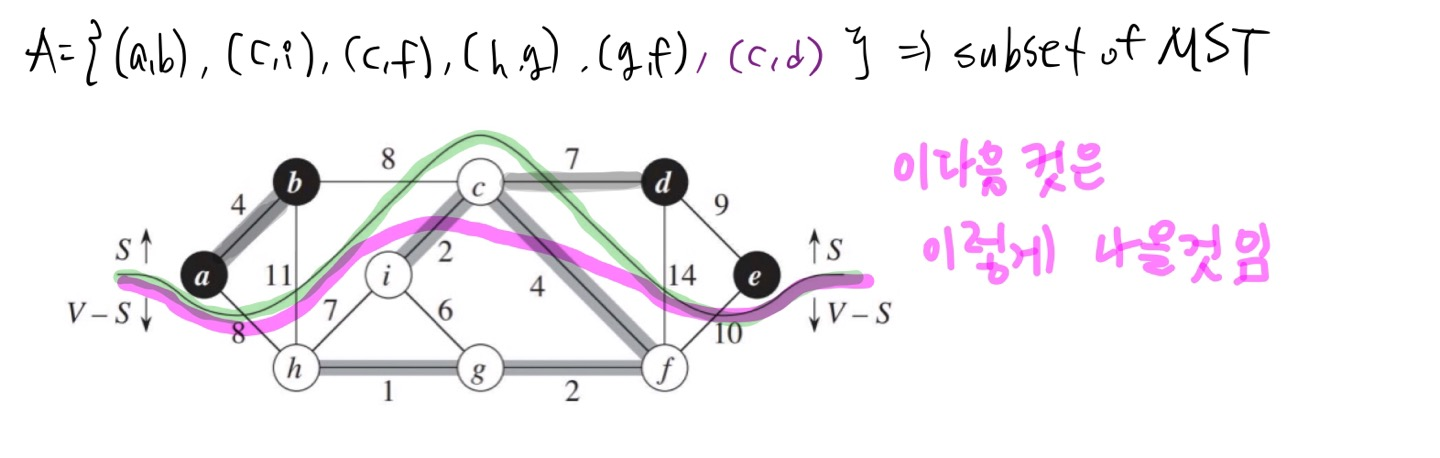
edge들의 집합 A를 만든다.
초기에 A는 공집합이다. --> A에 edge를 추가하면 이는 loop invariant를 유지한다.
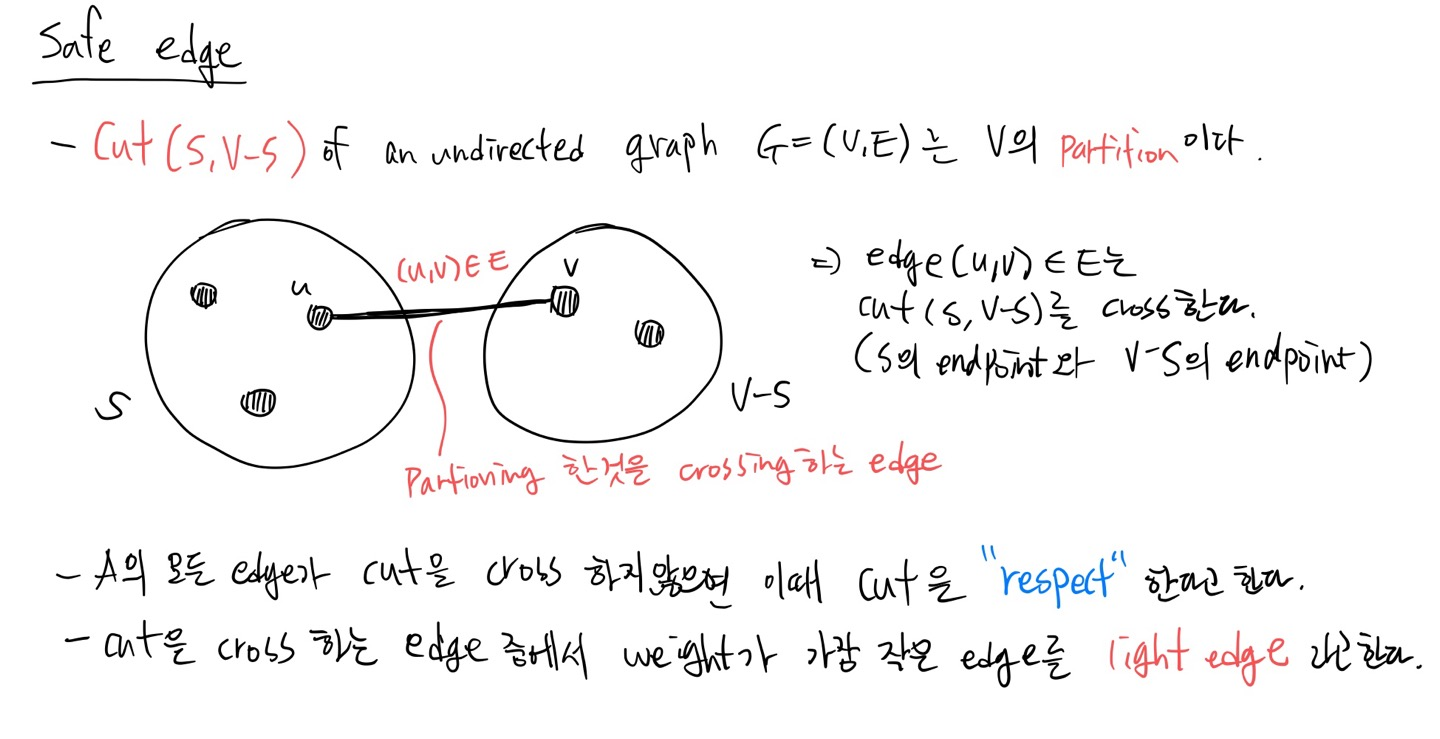
[loop invariant] A is a subset of some MST
- (u,v)가 safe edge 이면, A에 (u,v)를 추가했을 댸, MST의 subset이 된다.
- 그래서 오직 sage edge만 A에 추가한다.
- Initalization: 공집합은 모든 집합의 subset 이므로, loop invariant 만족함
- Maintenance: safe edge만 추가하므로 MST의 subset를 유지함
- Terminaiton: A에 추가하는 모든 edge는 MST에 있으니까 A는 MST이다.


Prim algorithm
- generic minumum-spanning-tree method의 special case임
- 그래프에서 가장 짧은 길을 찾는 다익스트라 알고리즘과 매우 비슷하게 작동함

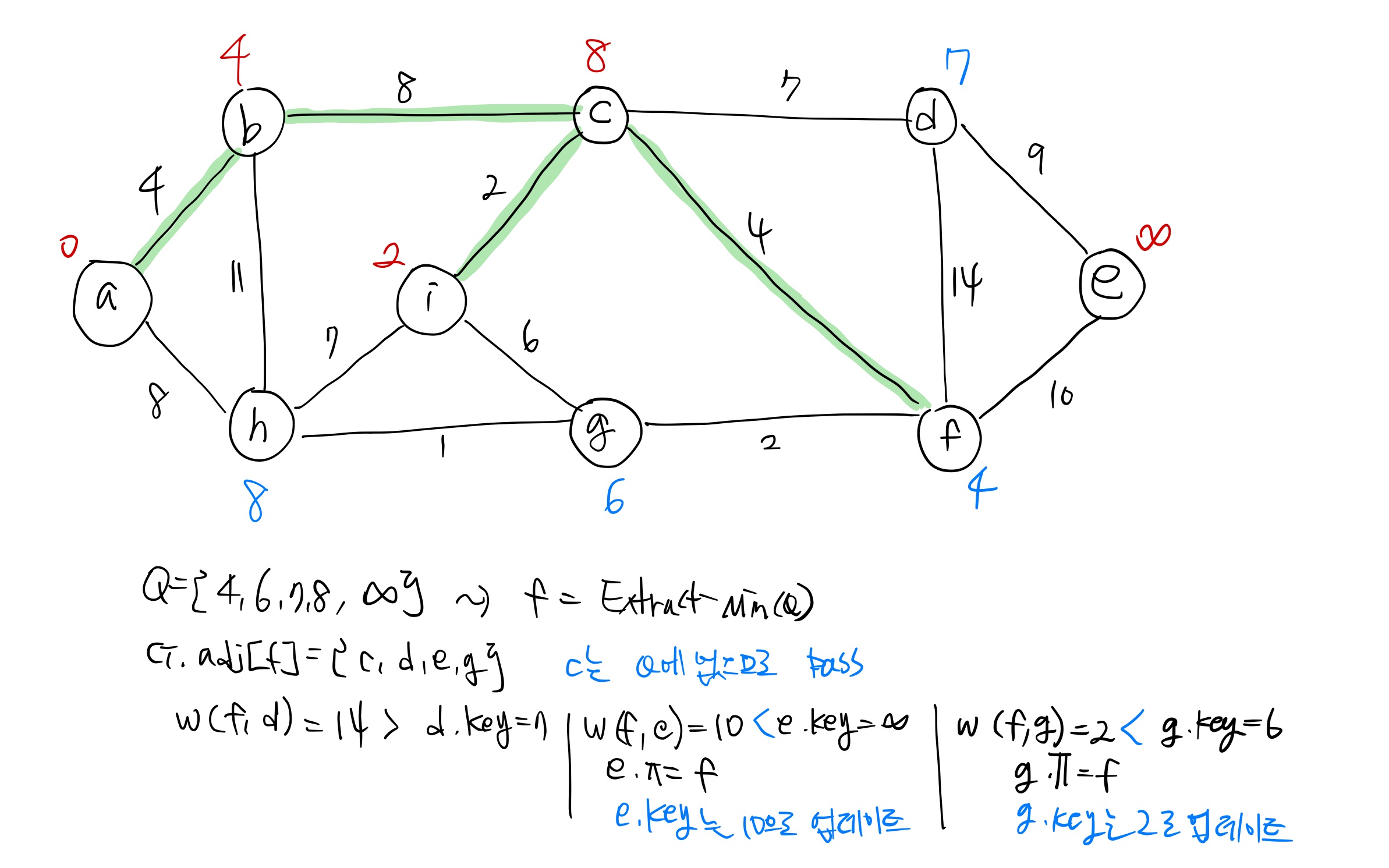
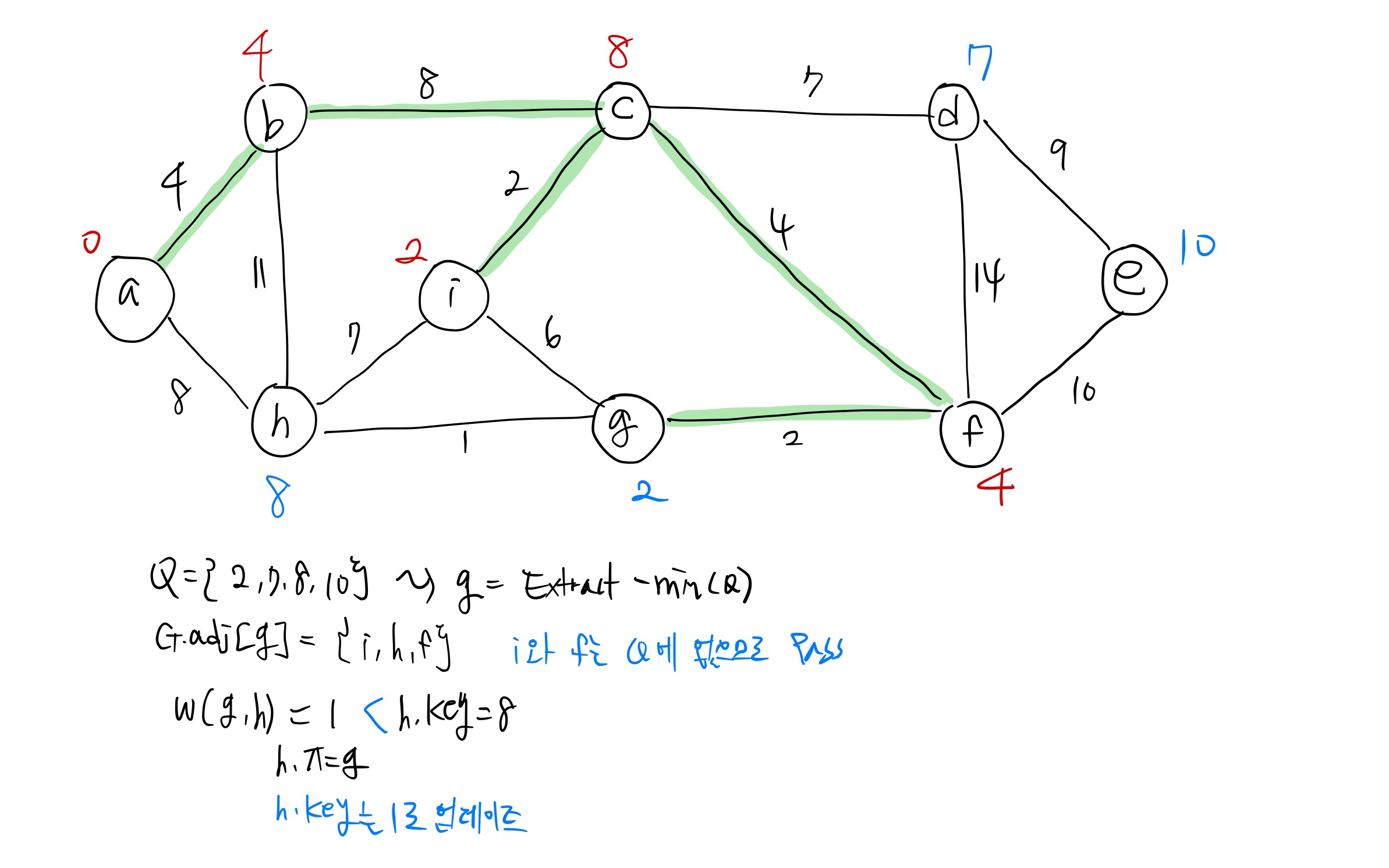
Prim's algorithm 예제






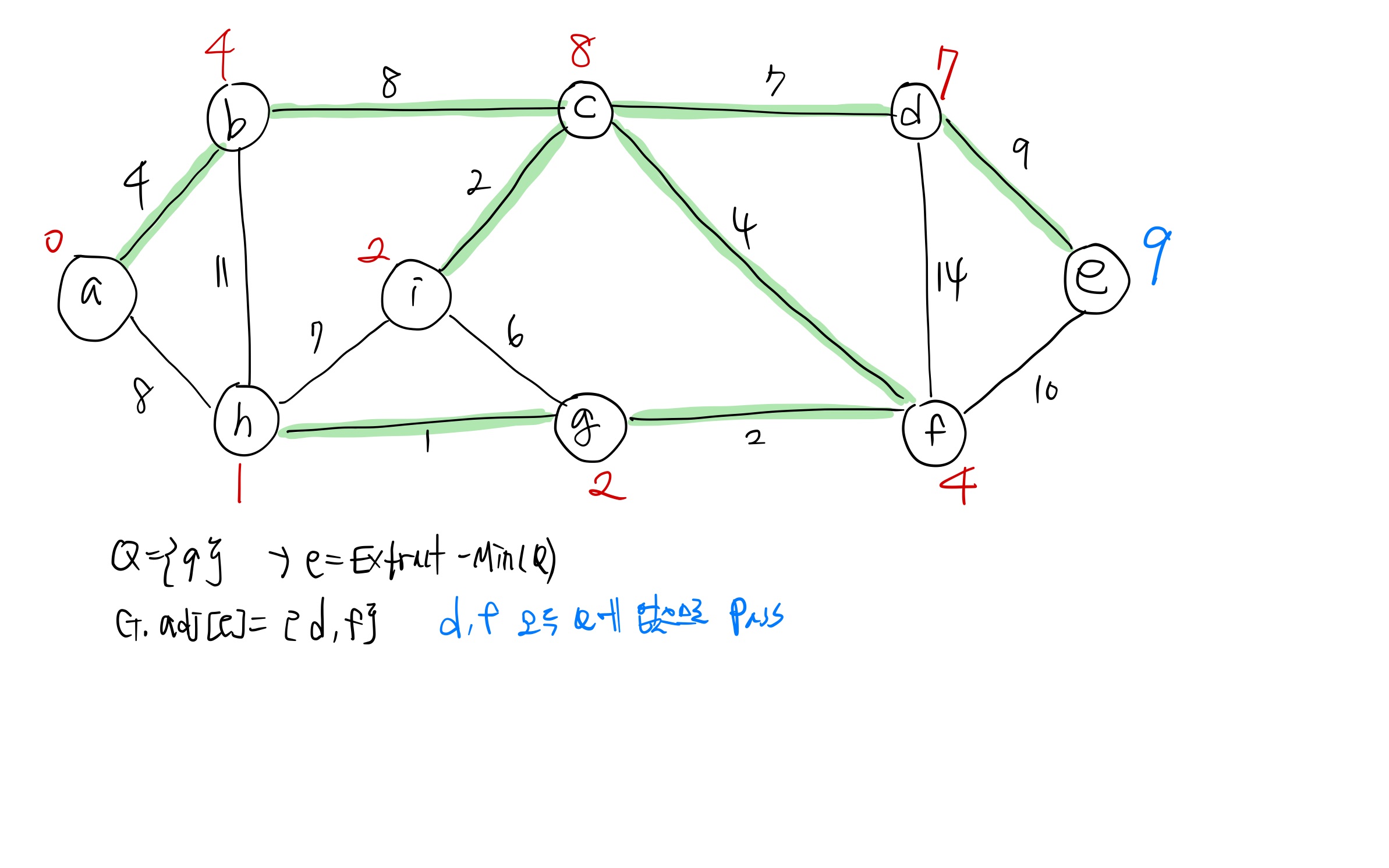
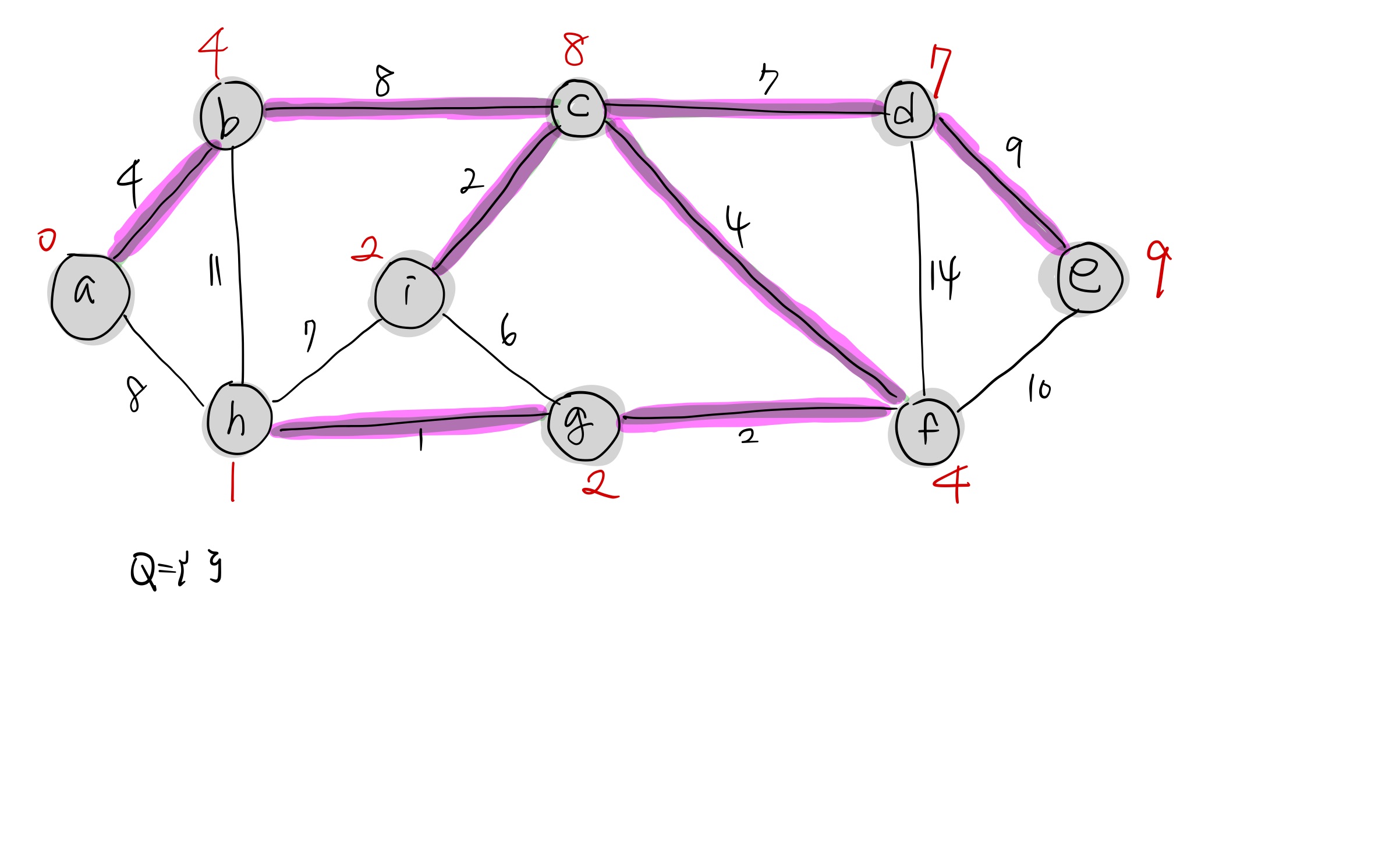
Performance of Prim's algorithms
: O(V log V + E log V) = O(E log V)
'Computer Science > algorithms' 카테고리의 다른 글
| [알고리즘] N-Queens problem : backtracking algorithm (0) | 2021.11.30 |
|---|---|
| [알고리즘] Maximum Flow : The Ford-Fulkerson method (0) | 2021.11.24 |
| [알고리즘] Network flow : BFS & DFS (0) | 2021.11.12 |
| [알고리즘] Huffman codes : greedy algorithm (0) | 2021.11.08 |
| [알고리즘] Greedy algorithm (0) | 2021.11.04 |
