(2021.10.08)
이번에 정리할 부분 목차
3.1 대칭키 암호
3.1.1 kerckhoff의 원리
3.1.2 암호 해독 공격
3.2 고전 암호의 분류
3.2.1 대치 암호
3.2.1.1 단일 문자 암호
3.2.1.2 다중 문자 암호
3.1 대칭키 암호
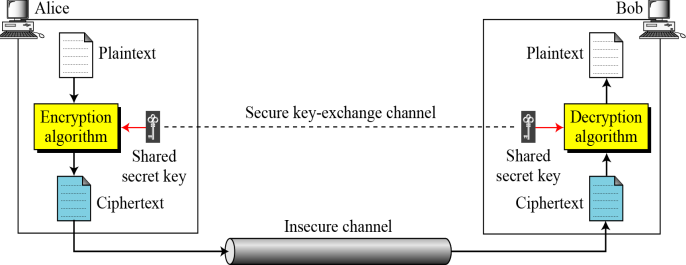
Alice가 Bob에게 보내는 상황
보내려는 메시지 원본: 평문(Plain text)
채널을 통해 전송하는 실제 메시지: 암호문(Cipher text)
평문------>암호문 을 만들기 위하여 Alice는
암호문 알고리즘(enctyption algorithm)과 비밀키(secret key) 사용
암호문----->평문 으로 복구하기 위해 Bob은
복호문 알고리즘(decrypthion algorithm)과 비밀키(secret key) 사용
(key는 암호가 동작하는데 필요한 값들의 집합임.)
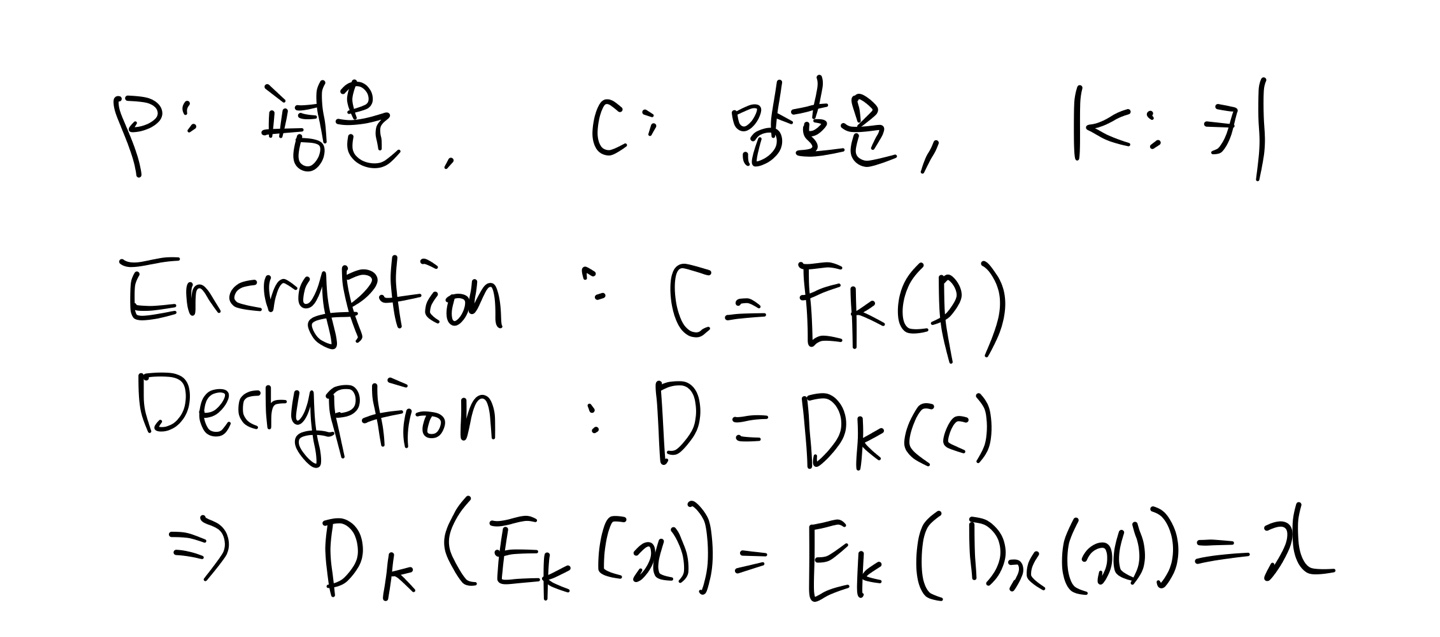
3.1.1 kerckhoff의 원리
공격자 Eve는 암호/복호 알고리즘을 알고 있다고 가정함.
공격에 대한 암호의 안전성은 키의 비밀성에만 기반을 두어야함.
(키를 추측하는 것이 매우 어려워서 암호/복호 알고리즘을 비공개로 할 필요가 없어야함.)
--> 현대 암호에서는 키 공간(key domain)이 매우 커서 공격자가 키를 추측하는 것이 어려움.
+ 교수님 강의노트에 있던 군사용 암호의 6가지 설계원칙
1. 암호체계는 수학적으로는 해독 불가능하지 않다고 하더라도, 실질적으로 그래야한다.
2. 암호체계는 비밀에 붙여질 필요가 없어야만하고, 적의 손에 떨어지더라도 문제가 없어야한다.
3. 키는 글로 쓰여지지 않더라고 교환 혹은 보관할 수 있어야한다.
4. 전신에 적용할 수 있어야한다.
5. 이동이 가능해야하고, 암호 체계의 사용과 기능을 위해 여러사람의 협력을 필요로 하지 않아야한다.
6. 시스템의 활용을 요구하는 여러 상황들이 주어졌을 때, 암호 체계는 이용이 쉬워야하고, 정신적인 압박감이나 여러 규칙들의 관찰을 필요로 하지 않아야한다.
3.1.2 암호 해독 공격
암호(cryptography)가 비밀코드를 생성하는 과학/기술 인 것처럼
암호해독(cryptanalysis)은 코드를 깨는 과학/기술 임.
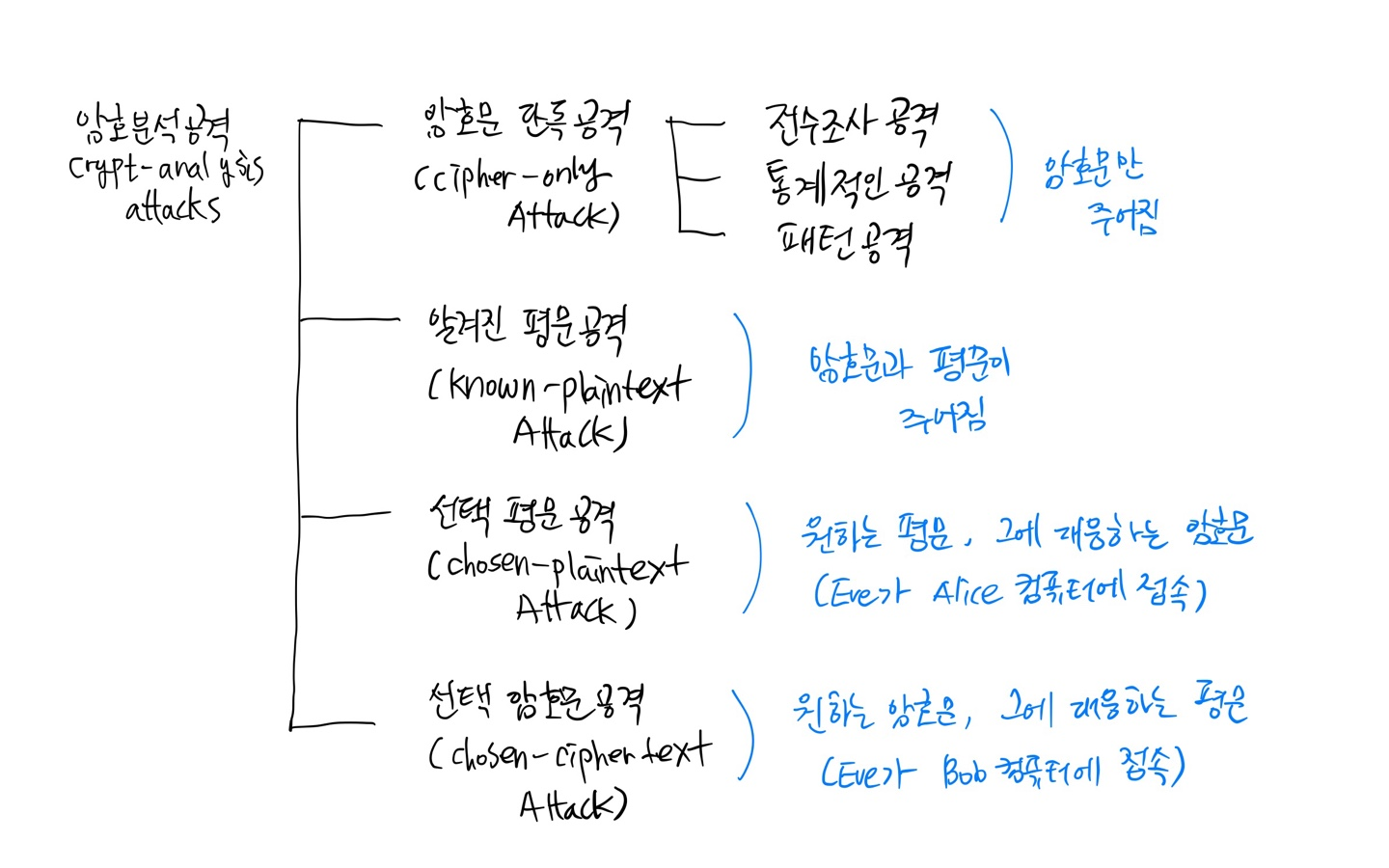
- 암호문 단독공격
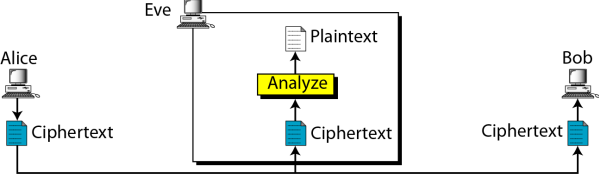
-- 전수조사 공격: Eve는 가능한 모든 키 사용 (공격막기 위해선 가능한 키의 수가 매우 커야함)
-- 통계적인 공격: 평문언어의 특징으로부터 정보 획득 (암호문이 평문 언어의 특징을 드러내지 않아야함)
-- 패턴 공격: 암호문에서의 존재가능한 패턴으로부터 정보 획득 (암호문을 랜덤하게 보이도록 만들어야함)
- 알려진 평문공격
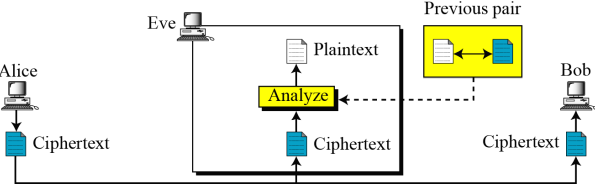
-- 해독하려는 암호문 외에 추가로 여러개의 평문/암호문 쌍 획득
-- Alice가 키를 변경하거나, 과거에 보낸 메시지를 노출하지 않는 등의 경우에는 적용 불가능함
- 선택 평문공격
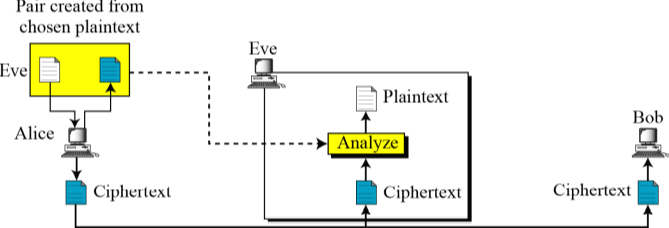
-- 자신이 원하는 평문을 선택하고, 이에 대응되는 암호문을 얻음
-- Eve가 Alice의 컴퓨터에 접속할 수 있어야함
-- 적용가능한 상황이 드뭄
- 선택 암호문공격
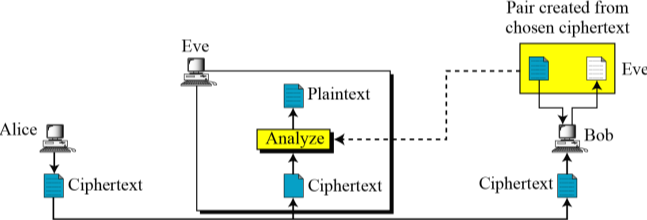
-- 자신이 원하는 암호문을 선택하고, 이에 대응되는 평문을 얻음
-- Eve가 Bob의 컴퓨터에 접속할 수 있어야함
-- 선택 평문 공격과 유사함
3.2 고전 암호의 분류

3.2.1 대치 암호
대치암호는 하나의 기호를 다른 기호로 대체한다.
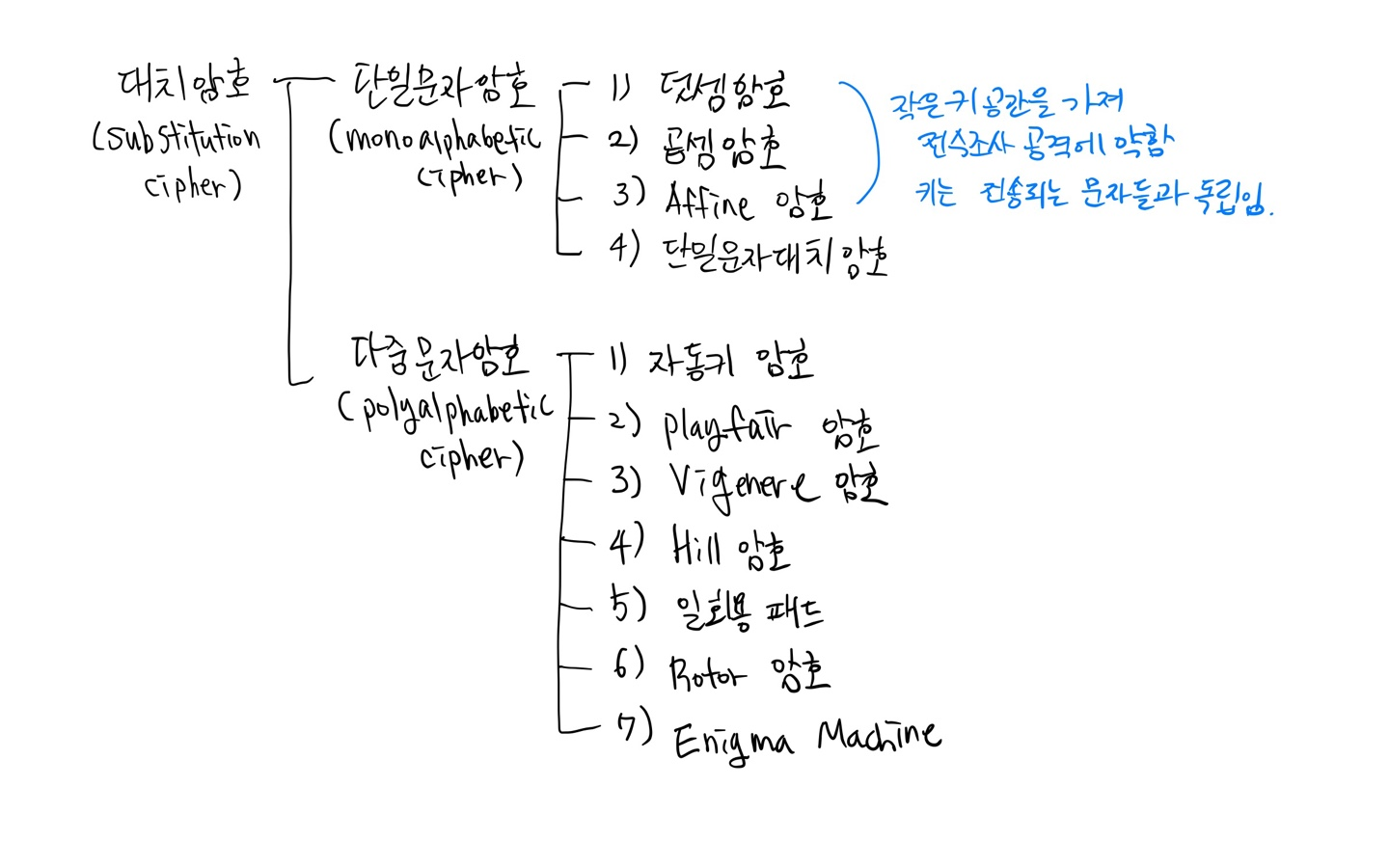
단일문자 암호(monoalphabetic cipher)
: 평문에서 하나의 문자/기호가 위치와 상관없이 암호문에서 항상 같은 문자/기호로 대체됨
: 작은 키 공간을 가져 전수조사 공격에 취약함
: Alice 와 Bob이 하나의 키를 공유한 후, 암호화와 복호와에 사용함 --> 키는 전송되는 문자들과 독립적임
: 평문의 문자/기호와 암호문에 대응되는 문자/기호는 항상 일대일 대응 관계를 가짐
- 덧셈 암호(additive cipher)
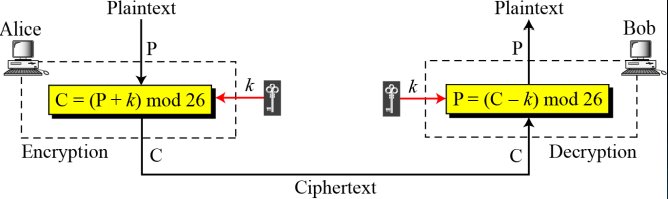
-- 이동암호, 시저암호라고도 함 (시저 암호는 키가 3인 암호)
-- 가장 간단한 단일 문자 암호
-- 전수조사 공격이 가능하며, 빈도수(통계적 공격)로 더욱 빠르게 암호를 해독할 수 있음
- 곱셈 암호(multiplicatiove cipher)
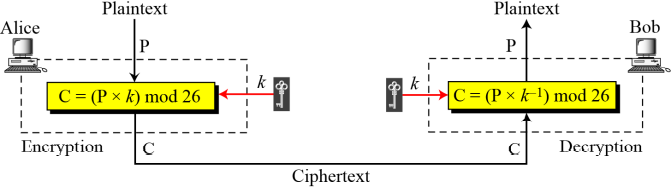
-- 평문에 키를 곱하고, 암호문은 키로 나눔
-- 모든 연산은 Z26에서 수행되는데, 복호화는 키의 곱셈에 대한 역원을 곱하는 것임
(평문과 암호문은 Z26의 원소이고, 키는 집합 Z26*의 원소여야함)
-- 키 공간 Z26* = { 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25 } : 총 12개의 원소
- 아핀 암호(affine cipher)
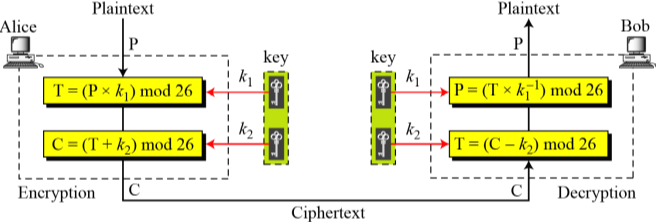
-- 두개의 키 사용, 덧셈암호와 곱셈암호를 결합함
-- 곱셈암호와 마찬가지로, 평문과 암호문은 Z26의 원소이고, 키는 Z26*의 원소임
-- 위의 그림에서 k1은 곱셈에 대한 역원이고, k2는 덧셈에 대한 역원임
- 단일문자 대치 암호

-- 평문 문자와 대응되는 암호문 문자 사이의 mapping을 구성하는 방식
-- 키 공간의 크기가 26! 이기 때문에 전수조사 공격하기에 힘이 듬
-- 문자의 출현 빈도수를 변경시키지 않아 통계적 공격에 취약함
다중문자 암호(polyalphabetic cipher)
: 각 문자가 다른 문자로 대치됨
: 평문 문자와 암호문 문자와의 관계는 일대 다 대응임
: 단일 문자 빈도 분석을 사용할 수 없어 통계적인 공격이 어려움
- 자동키 암호(auto key)

-- 자동키는 암호화 과정 중 부분키가 평문으로부터 자동으로 생성됨을 의미함
-- 첫번째 부분키는 Alice 와 Bob이 비밀리에 합의한 사전에 정의된 값이고, 두번째부터는 평문 값임
- playfair cipher
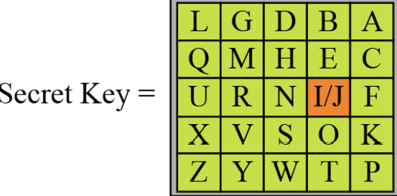
-- 평문을 두 문자씩 끊어서 두 문자가 연속해서 같으면, 그 사이에 가짜문자를 삽임함
-- 전체 문자의 개수가 홀수면, 맨 끝에 가짜 문자를 추가함
-- 두 문자가 같은 행일 경우 각각의 오른쪽 문자
-- 두 문자가 같은 열일 경우 각각의 아래 문자
-- 같은 열도 아니고, 같은 행도 아닐 경우 교차 했을 때 각각 같은 행의 다른 열의 문자
-- 키 공간의 크기가 25! 이므로 전수조사 공격이 어려움
-- 두 문자열 비교 테스트에 기반한 암호문 단독 굥격 사용가능
- Vigenere cipher
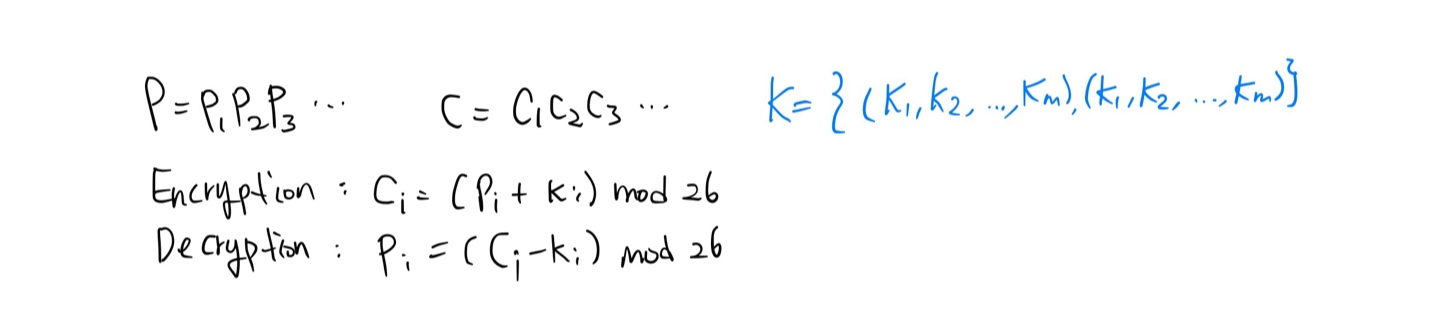
-- 길이가 m인 키 수열을 반복한 비밀 키를 이용한 덧셈암호 (덧셈암호는 m=1 인 비즈네르 암호)
-- m의 범위는 1≤m≤26 임
-- Vigenere 키 수열은 평문문자에 의존하지 않고, 평문의 문자 위치에만 의존함
-- 키 수열은 평문을 모르고도 생성가능함
-- Kasiski 테스트를 통해서 Difference의 최대공약수 = a, 키의 길이는 a의 배수임을 알아내어 해독할 수 있음
- Hill cipher
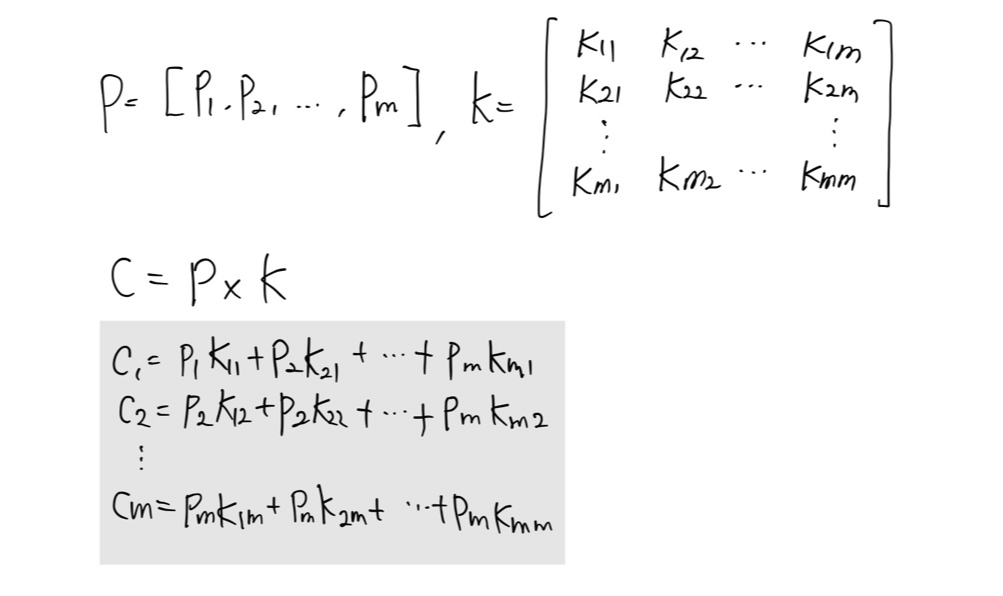
-- m x m 정방행렬을 키로 가짐
-- 키 행렬은 곱셈에 대한 역원을 가짐
-- 키가 m x m 행렬이기 때문에 키 공간의 크기는 26^(mxm)임 -> 암호문 단독 공격을 적용하기 어려움
-- 평문의 통계를 보존하지 않음 -> 통계적 공격 적용하기 어려움
- 일회용 패드(one-time pad:OTP)
-- 각 평문 문자가 키 공간에서 랜덤하게 키를 선책하여 암호화된다면, 완벽한 암호가 될 수 있음(Shannon의 연구)
-- 키와 평문의 길이가 같으며 완전히 랜덤하게 선택됨 -> 암호문 단독 공격 불가능
- Rotor cipher
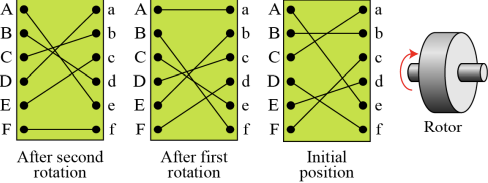
-- 3개의 일대일 대응 관계를 생성함
-- 키공간이 26! 임 -> 전수조사 공격에 안전함
-- 문자 빈도를 보존하지 않음 -> 통계적 공격에 강함
- Enigma Machine
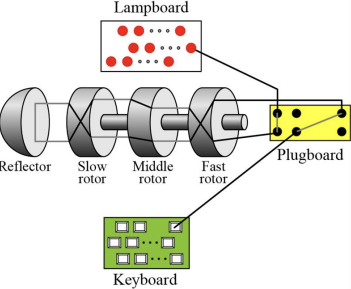
-- 에니그마 구성요소:(키보드, 램프보드, 플러그보드, rotor, 반사경)
-- 코드북: (5개의 rotor 중 3개, rotor의 설치 순서, 플러그보드의 설정, 그날의 세문자코드)
-- 암호화 과정 1) rotor의 시작점을 그날의 코드로 맞춤
2) 랜덤한 세 문자 코드를 선택하여 암호화
3) rotor의 시작점을 2)의 암호화된 코드의 반으로 놓음
4) 3)의 코드를 메시지 앞에 추가하여 암호문 만들어 전송
-- 복호화 과정 1) 메시지를 받고 첫번째의 6글자 분리
2) rotor의 초기 설정을 그날의 코드로 맞춤
3) 첫 6글자 해독(복호화)
4) rotor의 위치를 3)의 전반부로 설정
5) 나머지 메시지 해독(복호화)
'Security > 현대 암호학' 카테고리의 다른 글
| [현대암호학] 제 8장 - 현대 대칭키 암호 (블록암호&스트림암호) (0) | 2021.11.01 |
|---|---|
| [현대암호학] 제 3장 - 고전 대칭키 암호 (전치암호&스트림암호&블록암호) (0) | 2021.11.01 |
| [현대암호학] 제 2장 연습문제 (4) | 2021.10.04 |
| [현대암호학] 제 2장 암호수학(3) (1) | 2021.10.04 |
| [현대암호학] 제 2장 암호수학 (2) (0) | 2021.09.29 |
