(2021.09.21)
이번에 정리할 부분의 목차
2.1 정수연산(Integer Arithmetic)
2.1.1 정수 집합
2.1.2 이항 연산
2.1.3 정수의 나눗셈
2.1.4 가분성
2.1.5 선형 디오판투스 방정식
2.1 정수연산(Integer Arithmetic)
2.1.1 정수 집합
정수 집합(set of integers) 은 Z로 표현한다.
음의 무한대에서 양의 무한대까지의 모든 정수로 구성된 집합이다.
Z={,,, -2, -1, 0, 1, 2, ,,,}
2.1.2 이항 연산
이항 연산이란 2개의 입력값으로 1개의 결과값을 산출하는 연산이다.
일반적으로 이항 연산에는 덧셈, 뺄셈, 곱셈이 있다.
(나눗셈은 몫과 나머지라는 2개의 결과값을 산출하므로 이항 연산에 속하지 않음)
2.1.3 정수의 나눗셈
정수 연산에서 a를 n으로 나누면, 몫 q와 나머지 r을 얻는다.
a=qxn+r
(나눗셈은 연산이 아니고 나눗셈 관계식이다.)
☆ n은 양의 정수이며, r은 음이 아닌 정수이다.
2.1.4 가분성
a=qxn+r 에서 r이 0이면, n | a
r이 0이 아니면, n |/ a 라고 표시한다.
n | a 는 여러가지로 표현할 수 있다.
- n은 a를 나눈다. (n divides a)
- a는 n으로 나누어떨어진다. (a is divided by n)
- n은 a의 약수
- a는 n의 배수
정수 나눗셈의 특성
- a | 1 이라면, a=±1
- a | b 이고, b | a 이면, a=±b
- a | b 이고, b | c 이면, a | c
- a | b 이고, a | c 이면, a | (mxb + nxc) (m,n 은 임의의 정수)
유클리드 알고리즘
두수 a, b가 있을 때 (a>b) (r은 a를 b로 나눈 나머지)
gcd(a,b)=gcd(b,r)

확장 유클리드 알고리즘
두 정수 a,b가 있을 때 gdc(a,b) 뿐만 아니라
sxa + txb = gcd(a,b) 를 만족하는 s와 t를 구할 수 있다.
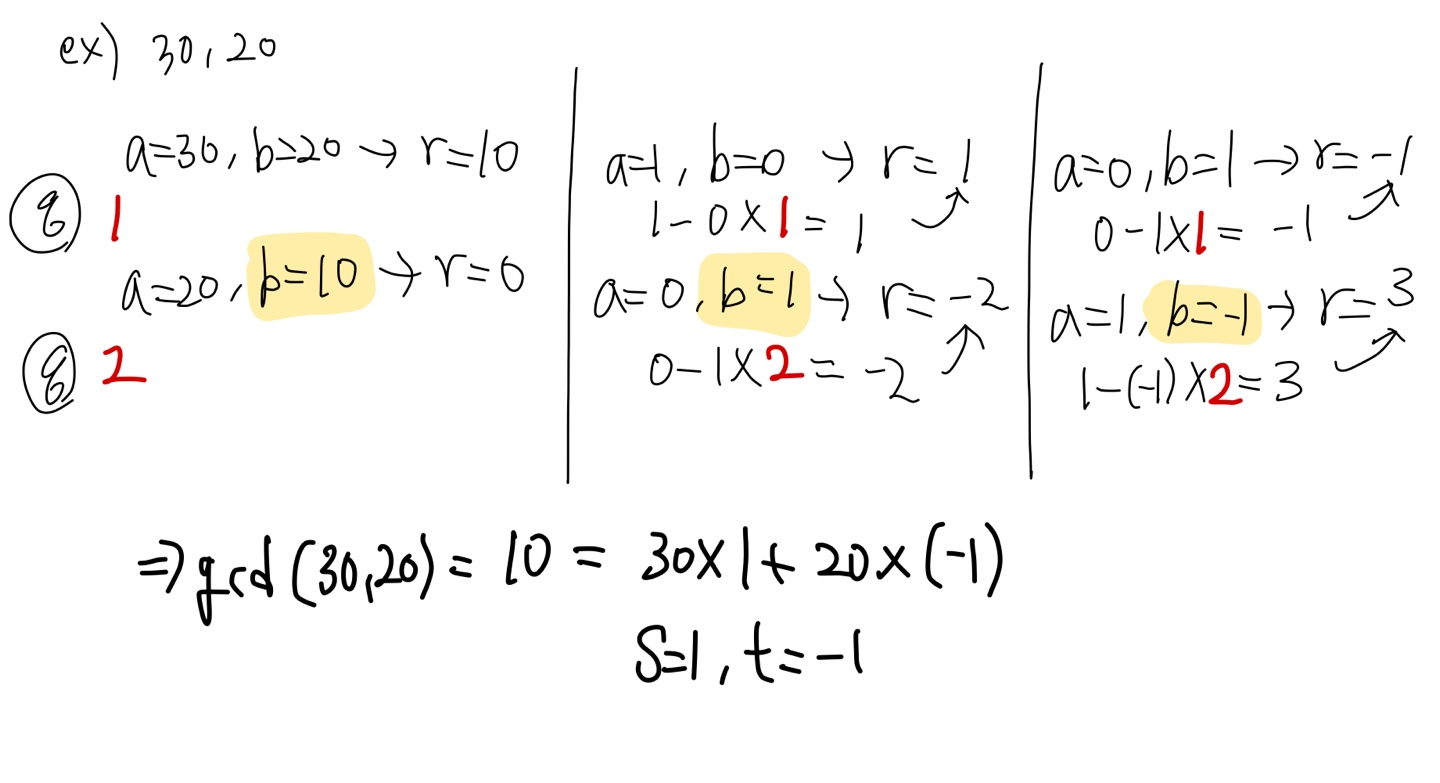
2.1.5 선형 디오판투스 방정식


728x90
'Security > 현대 암호학' 카테고리의 다른 글
| [현대암호학] 제 2장 암호수학(3) (1) | 2021.10.04 |
|---|---|
| [현대암호학] 제 2장 암호수학 (2) (0) | 2021.09.29 |
| [현대암호학] 제 2장 수학적 배경 (2) (0) | 2021.07.25 |
| [현대암호학] 제 2장 수학적 배경 (1) (0) | 2021.07.19 |
| [현대암호학] 제 1장 암호학 (0) | 2021.07.13 |
