(23.03.31)
algorithms S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani (2008) 책 읽고 정리하기
http://algorithmics.lsi.upc.edu/docs/Dasgupta-Papadimitriou-Vazirani.pdf
정리한 내용
6.5 chain matrix multiplication
chain matrix muliplication
- 행렬 곱셈 연산에서 곱셈 순서를 다르게 하면, 곱셈 cost도 달라지는데 최소의 cost로 곱셈 연산을 할 수 있도록 하는 방법을 dynamic programming 알고리즘을 통해서 알아낼 수 있다.
- 아래와 같이 A, B, C, D 행렬의 곱셈 순서를 다르게 하면 cost가 다르다.
- The order of multiplications makes a gib difference in the final running time!!!!

- dynamic programming의 sub-problem을 정의해보면 아래와 같다.
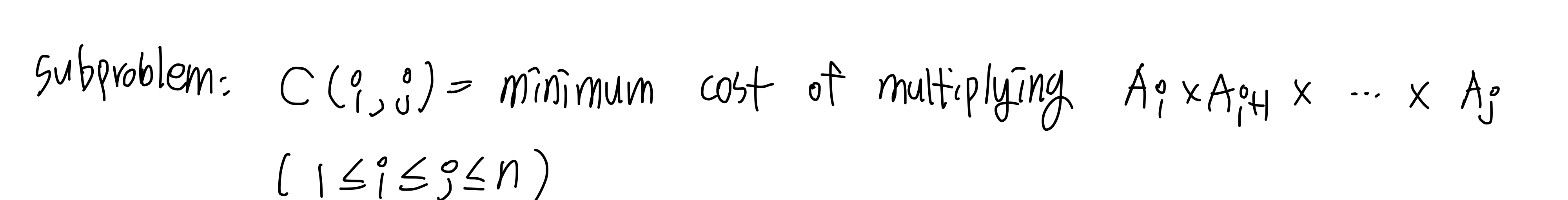
- C(i, j)를 binary tree로 표현하면, 아래와 같다.

- 이 binary tree를 k를 기준으로 둘로 쪼개면 아래와 같이 표현할 수 있다. m은 matrix를 곱하는 cost이다.

- chain matrix manipulation 알고리즘

- 또한, 이를 2-dimension table로 탐색할 수 있는데, 이때 총 시간 복잡도는 O(n^3)이다.
'Computer Science > algorithms' 카테고리의 다른 글
| [algorithms] 비교 기반 정렬 알고리즘 (선택정렬, 삽입정렬, 퀵정렬) (0) | 2023.05.14 |
|---|---|
| [algorithms] 시간복잡도 (0) | 2023.05.11 |
| [algorithms] ch6. Dynamic programming (Knapsack) (0) | 2023.03.30 |
| [algorithms] ch6. Dynamic programming (Edit distance) (0) | 2023.03.29 |
| [algorithms] ch6. Dynamic programming (shortest paths in dags, longest increasing subsequences) (0) | 2023.03.29 |
