(23.03.20-22)
algorithms S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani (2008) 책 읽고 정리하기
http://algorithmics.lsi.upc.edu/docs/Dasgupta-Papadimitriou-Vazirani.pdf
정리한 내용
5.1 Minimum spanning trees
-> kruskal's algorithm
-> cut property
-> Union Find
Greedy algorithm
매 순간마다의 최선의 선택을 하는 방법인데, 매순간마다의 그 최선의 선택이 결국 최종적으로 최선의 선택이 된다는 보장은 없다.
top-down 방식으로 최선의 선택을 하는 것이다.
다시 말하면 아래와 같다.
"solution set에 넣을 next item을 선택한다. 각각의 단계에서 최적의 선택을 한다."
"locally optimal solution을 찾음으로써 최종적으로 global optimal solution을 구하는 방법"
-> 최종 선택이 전체적으로 봤을 때 100% 최적의 선택이라고 말할 수는 없다.
그런데, greedy algorithm으로 최적의 솔루션을 도출하는 문제들이 있다. (kruskal's algorithm)
Spanning Tree
- connected, undirected graph, acyclic
- 무방향 그래프의 최소 연결 그래프라고 말할 수 있다. 그래프에서 일부 edge를 선택해서 만든 트리!!
- 그래프인데, 모든 정점을 포함하면서, 그 정점들이 모두 연결되어있고, 이를 연결하는 edge의 수는 최소인 트리 형태가 바로 spanning tree이다.

Minimum spanning tree
- spanning tree 중에서 edge의 가중치들의 합이 최소가 되는 tree를 말한다.

Kruskal's minimum spanning tree algorthm
- greedy 방식으로 네트워크의 모든 node를 최소 비용으로 연결하는 최적의 답을 구하는 알고리즘이다.
---> empty graph에서 시작해서 E의 edge들을 골라내서 최종 tree를 완성하는 방식이다.
- edge를 고르는 조건은 가장 lightest하고, cycle을 만들지 않는 edge이다.
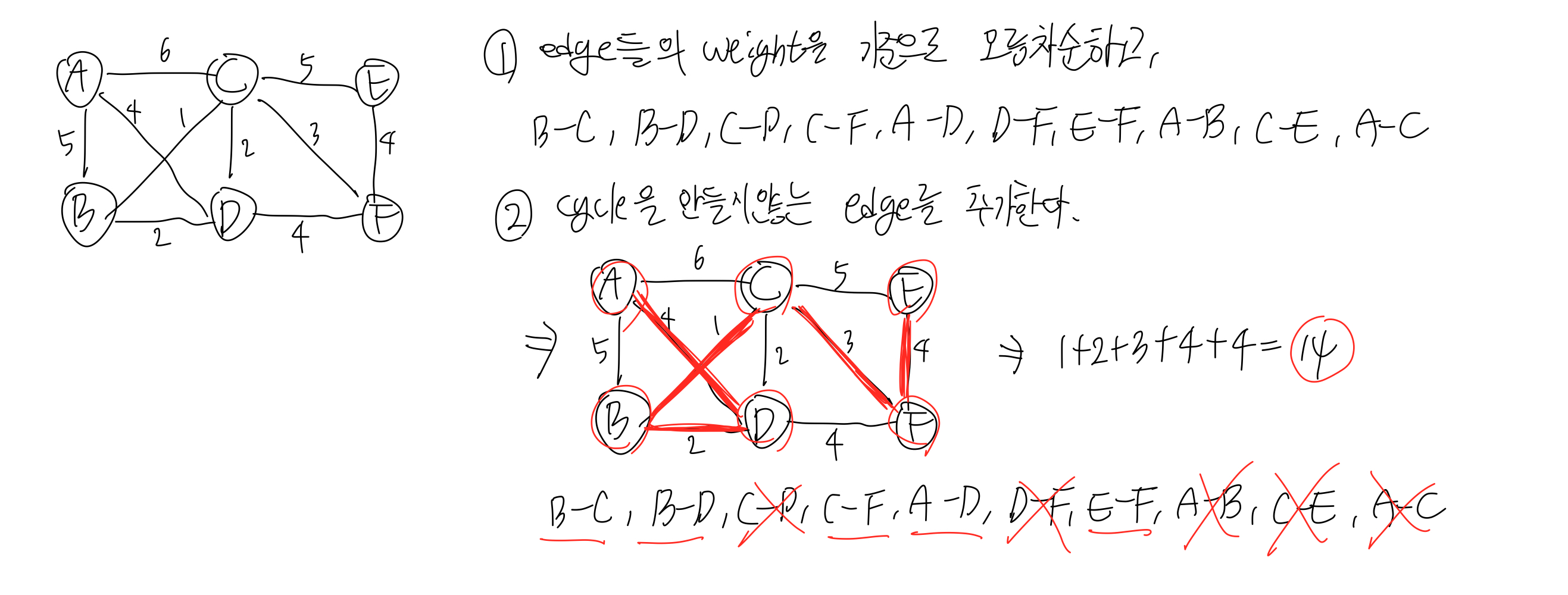
kruskal's minimum spanning tree 알고리즘의 동작 단계
1) edge들의 weight을 기준으로 edge들을 오름차순 정렬한다.
2) 오름차순 정렬한 edge들을 하나씩 고르는데 cycle이 만들어지지 않도록 한다.
3) 선택한 edge를 MST(최소 비용 신장 트리)의 집합에 추가한다.
---> 여기에서 kruskal's algorithm의 correctness에 대한 증명을 해주는 것이 cut property 이다.
---> 여기에서 cycle이 만들어지지 않는지를 확인하는 방법이 있다: Union-Find
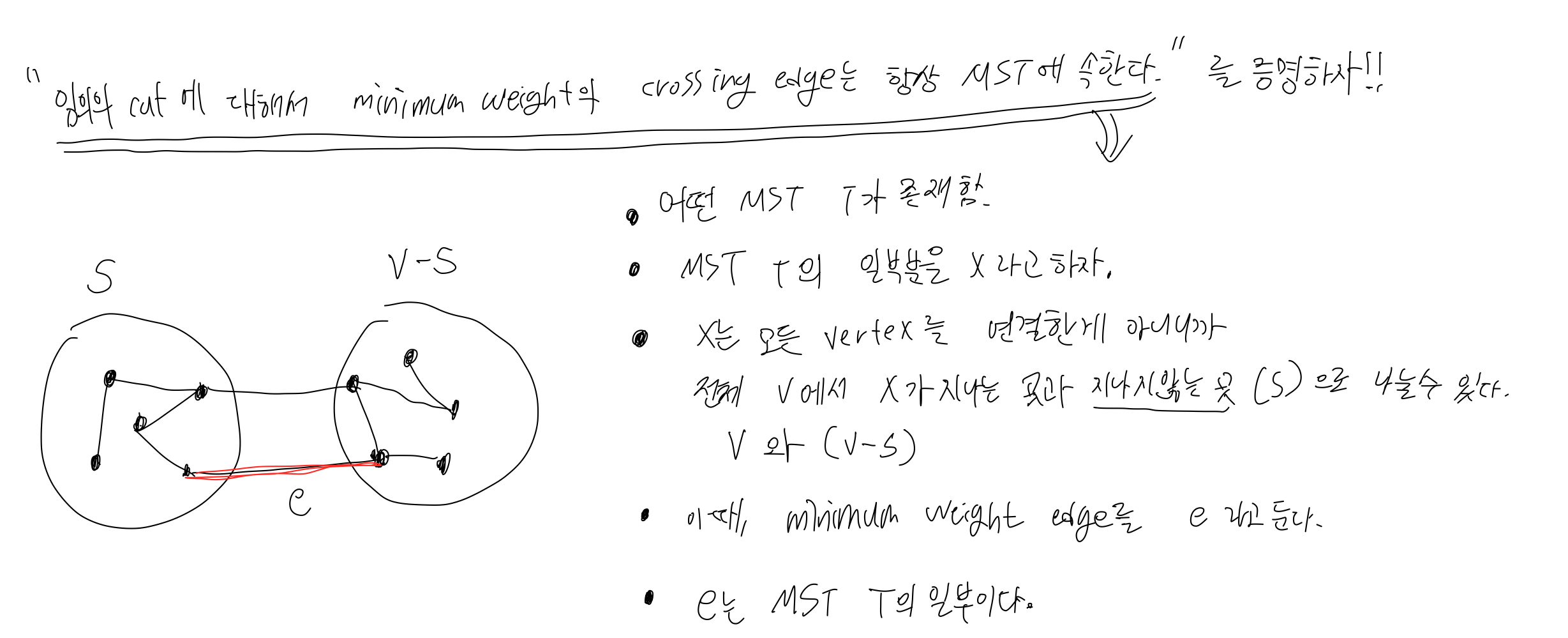
The cut property
cut은 2개의 set으로 나눈 vertex의 집합이다.
각각의 집합에서 하나의 vertex씩 연결한 edge를 crossing edge라고 한다.
임의의 cut에서 minimum weight crossing edge는 항상 MST에 속한다는 것이 cut property이다.
(뭔가 당연한걸 증명하려고 하니까 어렵다)

Union-Find
: cycle을 형성하는지 판단할 수 있도록 하는 자료구조
kruskal's 알고리즘은 edge (u,v)를 고를 때, 다른 component에서 u와 v를 고르고, 고른 뒤에는 u가 속하는 component와 v가 속하는 component 가 합쳐진다. -> Union Find는 이를 위한 기능을 가지고 있다.
makeset(x): x만을 원소로 가지는 집합생성
find(x): x가 속한 집합 찾기
union(x, y): x가 속합 집합과 y가 속한 집합 합치기

find(u) 와 find(v) 를 비교하여 같지 않을 경우, union(u, v) 연산을 해주어 집합을 합쳐준다.
( |V| makeset, 2|E| find, |V|-1 union operations )
Union-Find 는 각 set을 directed tree로 구현한다.
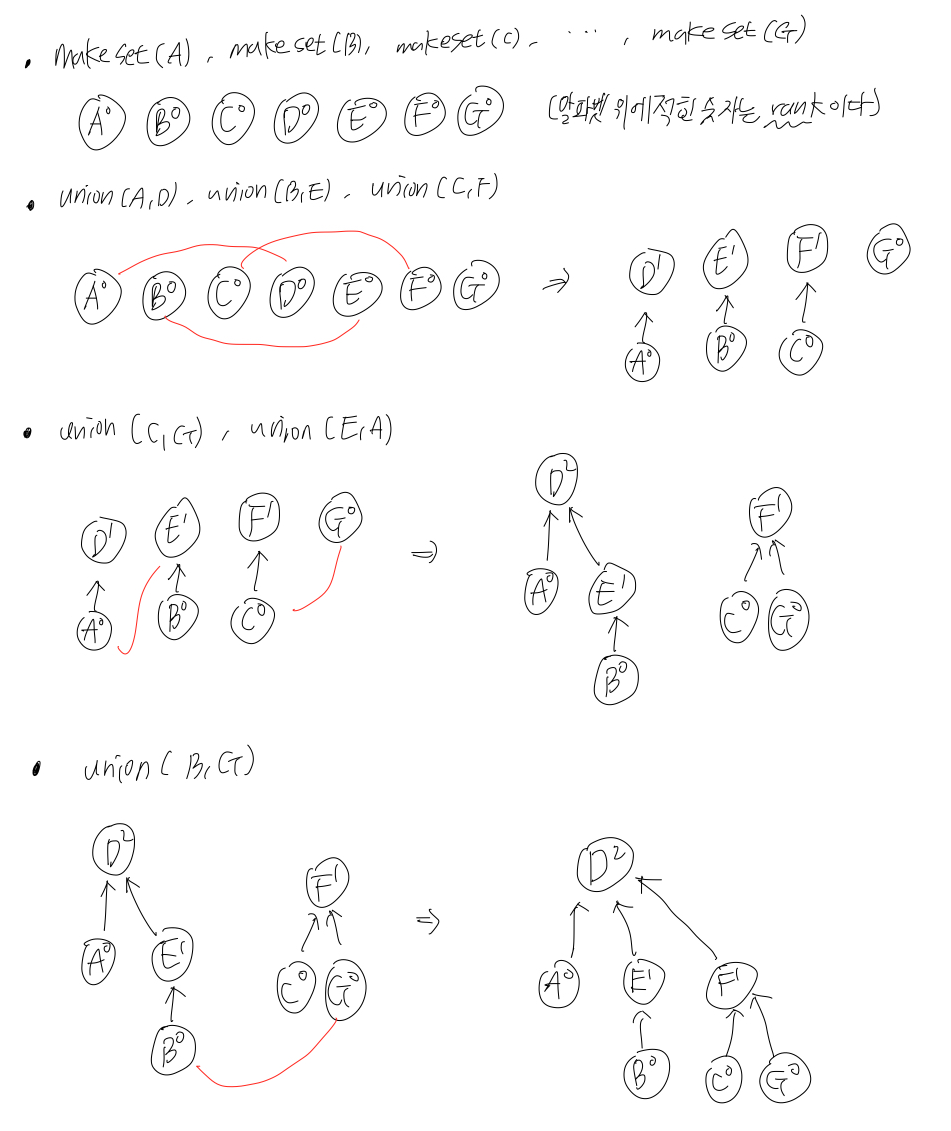

x를 root 로 가지는 tree 만든다. 그리고 rank는 0으로 둔다.

root에 도달할 때까지 찾아서 반환한다.

Kruskal's algorithm python code
# kruskal's algorithm - Minimum Spanning Tree
# Union-Find
def makeset(parent, rank, v):
parent[v] = v
rank[v] = 0
def find(parent, v):
if parent[v] != v:
parent[v] = find(parent, parent[v])
return parent[v]
def union(parent, rank, v1, v2):
root1 = find(parent, v1)
root2 = find(parent, v2)
if root1 != root2:
if rank[root1] > rank[root2]:
parent[root2] = root1
else:
parent[root1] = root2
if rank[root1] == rank[root2]:
rank[root2] += 1
def kruskal(graph):
parent = dict()
rank = dict()
mst = []
for v in graph['vertex']:
makeset(parent, rank, v)
# sorting edge's weight
edge = graph['edge']
edge.sort()
for e in edge:
w, v1, v2 = e
if find(parent, v1) != find(parent, v2):
union(parent, rank, v1, v2)
mst.append(e)
return mst
if __name__ == '__main__':
graph = {
'vertex': ['A', 'B', 'C', 'D', 'E', 'F', 'G'],
'edge': [
(7, 'A', 'B'),
(5, 'A', 'D'),
(7, 'B', 'A'),
(8, 'B', 'C'),
(9, 'B', 'D'),
(7, 'B', 'E'),
(8, 'C', 'B'),
(5, 'C', 'E'),
(5, 'D', 'A'),
(9, 'D', 'B'),
(7, 'D', 'E'),
(6, 'D', 'F'),
(7, 'E', 'B'),
(5, 'E', 'C'),
(7, 'E', 'D'),
(8, 'E', 'F'),
(9, 'E', 'G'),
(6, 'F', 'D'),
(8, 'F', 'E'),
(11, 'F', 'G'),
(9, 'G', 'E'),
(11, 'G', 'F')
]
}
print(f'kruskal algorithms: {kruskal(graph)}')
https://github.com/gompaang/algorithm_python/blob/master/kruskal.py
GitHub - gompaang/algorithm_python
Contribute to gompaang/algorithm_python development by creating an account on GitHub.
github.com
'Computer Science > algorithms' 카테고리의 다른 글
| [algorithms] ch5. Greedy algorithms (Huffman encoding) (0) | 2023.03.25 |
|---|---|
| [algorithms] ch5. Greedy algorithms (MST: prim algorithm) (0) | 2023.03.24 |
| [algorithms] ch4. Paths in graphs (Bellman-Ford's algorithm) (4) | 2023.03.19 |
| [algorithms] ch4. Paths in graphs (Dijkstra's algorithm, priority queue, heap) (0) | 2023.03.17 |
| [python] DFS, BFS 구현 (0) | 2023.03.16 |
