(23.03.01)
선형대수 정리하기 6탄
eigenvalue와 eigenvector의 정의

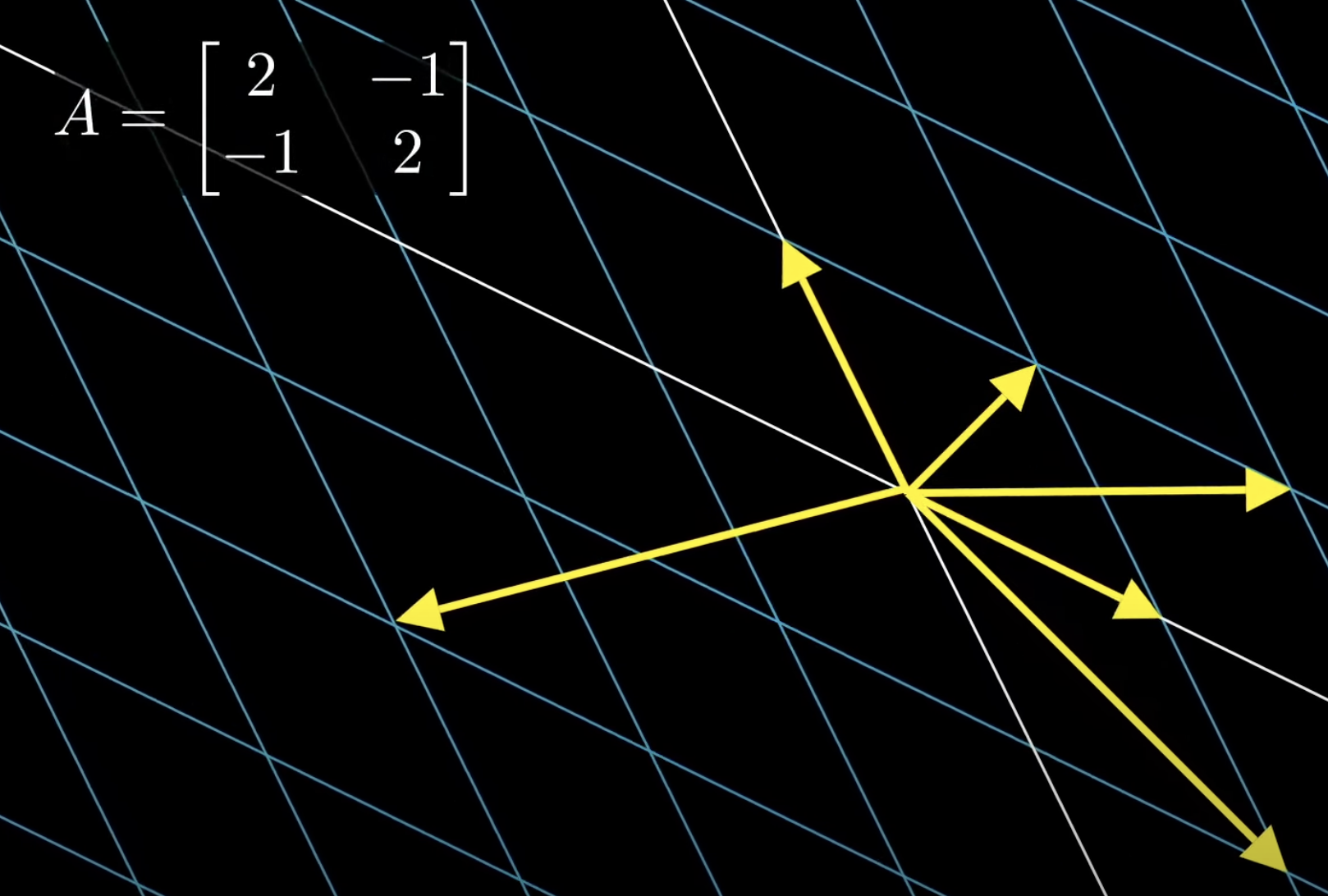
여기서 A라는 것은 선형변환이라고 생각하면된다.
회색 벡터를 A에 통과시키면 노란색 벡터가 나온다.

아래 그림을 보면 노란색 벡터가 파란색 좌표들에 그려진 것을 볼 수 있다.
아래 그림의 회색선이 기존의 좌표선들이고, 파란색선이 새로운 좌표선들이다.

아래 두그림을 비교해봤을 때, 방향이 바뀌지 않은 노란색 벡터 두개를 확인할 수 있다.
방향이 바뀌지 않은 노란색 벡터 두개가 바로 eigenvector이다.

eigenvalue와 eigenvector 구하기

eigenvalue, eigenvector 구하기 예제



<명강의>
위의 그림의 출처는 이 유튜브 강의임!!
https://www.youtube.com/watch?v=xDARfmKauuA&list=PL_iJu012NOxdZDxoGsYidMf2_bERIQaP0&index=20
728x90
'Computer Vision > Mathematics' 카테고리의 다른 글
| [Linear Algebra] SVD (Singular Value Decomposition) (0) | 2023.04.24 |
|---|---|
| [Linear Algebra] eigen decomposition (고윳값 분해) (0) | 2023.03.02 |
| [Linear Algebra] trace, least squares, projection matrix (0) | 2023.02.28 |
| [Linear Algebra] 가우스-조던 소거법, 역행렬 증명, determinant (0) | 2023.02.28 |
| [Information theory] Entropy, KL divergence, Mutual Information (0) | 2023.01.27 |
