(23.01.27)
선형대수 정리하기 1탄
행렬의 기본 개념

행(row)는 가로, 열(column)은 세로라고 생각하면 된다.
=> 가로 2줄, 세로 3줄의 행렬은 2x3 크기를 가진 행렬이다.

행으로만 이루어진 벡터, 즉 가로만 있는 벡터를 row vector (행벡터)라고 부르고,
열로만 이루어진 벡터, 즉 세로만 있는 벡터를 column vector (열벡터)라고 부른다.

어떤 실수 a,b에 대해서 위의 식으로 2차원 좌표평면의 모든 것을 표현할 수 있다.
Transpose - 전치

전치는 어렵지 않은 개념인데,
행렬에서 하나의 요소를 a_ij라고 표현했을 때, 전치시키면 같은 자리의 요소가 모두 a_ji가 된다.
즉, 오른쪽 아래 방향의 대각선은 그대로 있게 된다. (i와 j가 같은 숫자니까)

전치시켜도 전치시키기 전과 같은 행렬을 symmetric matrix라고 한다.
transpose와 관련하여 몇가지 알아둘 내용은 아래와 같다.

Dot product & projection

transpose 개념과 엮어서 생각해볼 수 있다.

dot product 연산 과정을 보면, projection 해서 나온 스칼라값을 곱해주는 것을 확인할 수 있다.
또한, 벡터의 크기를 나타낼 수 있는 또 다른 표현법을 도출해낼 수 있다.
마찬가지로 단위벡터의 분모를 표현할 수 있다.
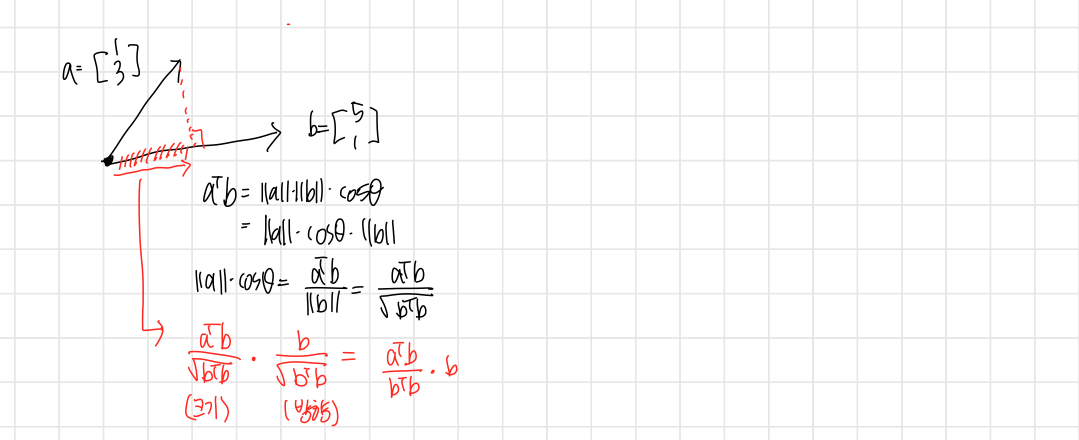
728x90
'Computer Vision > Mathematics' 카테고리의 다른 글
| [Linear Algebra] trace, least squares, projection matrix (0) | 2023.02.28 |
|---|---|
| [Linear Algebra] 가우스-조던 소거법, 역행렬 증명, determinant (0) | 2023.02.28 |
| [Information theory] Entropy, KL divergence, Mutual Information (0) | 2023.01.27 |
| [Linear Algebra] identity, inverse, diagonal matrix & rank & null space (0) | 2023.01.27 |
| [Linear Algebra] norm, linear combination, span, basis, linearly independent (0) | 2023.01.27 |
