(2021.10.14)
알고리즘 수업들으면서 정리하기 12탄
7주차 실강 내용- rod cutting problem
(손글씨가 아닌 모든 첨부사진은 교수님 강의노트가 출처-알고리즘 교재)
Rod cutting problem 설명하시기 전에
왜 dynamic programming인가?? 에 대한 수업을 하셨다
Why dynamic programming??
duplicate computation(반복적인 계산)이 많을 때, dynamic programming이 아주 효과적임!
예를 들어 생각하면 이해하기 쉽다.

n개에서 k개를 고르는 이항정리 문제는 위와 같이 표현할 수 있다. 이것으로 코드를 만들어본 것이 아래다.


C(n,k)=C(n-1,k-1)+C(n-1,k)에서
다시 C(n-1,k-1)과 C(n-1,k)는 각각 나눠진다.
위의 사진을 보면, 같은 계산을 요구하는 것이 보인다.
이와 같은 문제를 dynamic programming으로 해결해보면,

한번 계산한 결과는 다시 계산할 필요없이 다음단계에서 값만 가져다가 계산해나갈 수 있다.
중복된 계산을 없애준다는 점에서 dynamic programming을 사용하는 것이 훨씬 효과적이다.
Rod cutting problem
(사실 이거는 이해가 잘 안간다)
길이에 따른 가격이 정해져있는 파이프가 있다. 이때, 길이가 n인 파이프를 잘라서 최대 가격을 도출할 수 있는지 물어보는 문제이다.
input: A rod of length n inches and a table of prices pi for i=1,2,..,n
output: The maximum revenue obtainable for rods whose lengths sum to n, computed as the sum of the prices for the individual rods

간단한 예인데, 위와 같은 경우는 길이가 4인 파이프를 잘랐을 때, 최대 가격은 길이가 2인 파이프 2개로 자르는 경우이다. 이때 가격은 table에 나와있는 값에 따라 5+5=10 이된다.
근데 table에서 안잘랐을 때의 파이프(길이가 n인 파이프)의 가격이 정말로 충분히 크다면, 이때는 파이프를 자르지 않아도 된다.
파이프는 총 2^(n-1) 가지의 방법으로 자를 수 있다. (맨 앞부터 길이=1 하나씩 자르냐 마느냐)
ri: 길이가 i인 파이프의 최대 가격
pi: 자르지 않았을 때의 가격
r1+rn-1: 길이가 n인 파이프를 길이가 1이고, 길이가 n-1인 파이프로 잘랐을 때의 최대 가격
r2+rn-2: 길이가 n인 파이프를 길이가 2이고, 길이가 n-2인 파이프로 잘랐을 때의 최대 가격
...
결국, 최종적인 파이프의 최대가격은 max(pn,r1+rn-1,r2+rn-2,...,rn-1_r1) 이 된다.
optimal substructue
- 사이즈가 n인 original problem을 풀기 위해서, n보다 작은 사이즈의 subproblem들을 푼다.
- 자르고 나면, 두개의 subproblem이 생긴다. 그 두개의 subproblem은 서로 독립적이다.
- subproblem의 optimal solution이 original problem의 optimal solution에 영향을 준다.
recursive structure
- 모든 optimal solution은 가장 왼쪽을 자른다. (↓이런식으로)

- 왼쪽에 자른 것은 더이상 자르지 않고, 오른쪽만 더 잘라준다. ( 두 개가 아닌 한 개의 subproblem만 남기는 것)
- 아예 자르지 않은 경우는 i=n 인 것
---> max(pi+rn-i) (1≤i≤n)
recursive solution
반복적인 해결은 정말 효율적이지 않다. 같은 계산이 계속해서 반복된다.

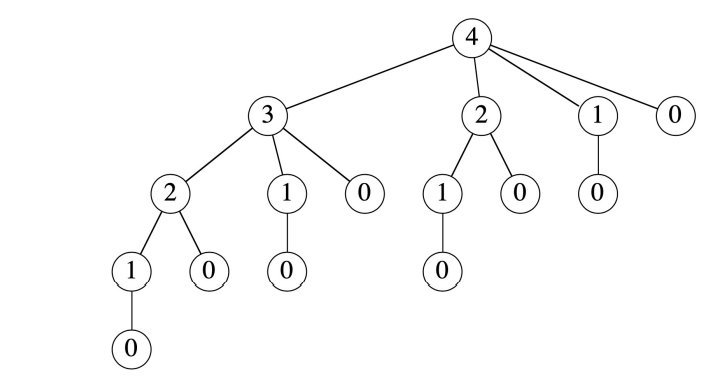
길이가 4일 경우에는 위의 그림과 같은 구조로 recursive 하게 풀 수 있는데 매우 비효율적이다.
T(n)을 CUT_ROD(p,n)을 호출하는 횟수로 둔다.


Dynamic-programming solution
d.p에서는 각각의 subproblem을 계산해서 table에 넣을 거니까 한번씩만 계산해도 된다.
recursive solution은 top-down방식이었다면,(n부터 n-1,n-2,....) dynamic-programming solution은 bottom-up방식이다.(작은값부터 큰값으로)

이렇게 하면 BOTTOM-UP-CUT-ROD(p,n)의 런타임은 세타(n^2)이다.
(왜냐면, for 문이 중첩되어있는데, j는 1부터 n까지고, 그 안의 for문에서 i는 1부터 j까지니까 1+2+3+...+n-1+n 번 실행되므로, nxn=n^2 이다.)
reconstruction a solution
1. save the optimal choices in a separate table
2. then use a separated procedure to print the optimal choices


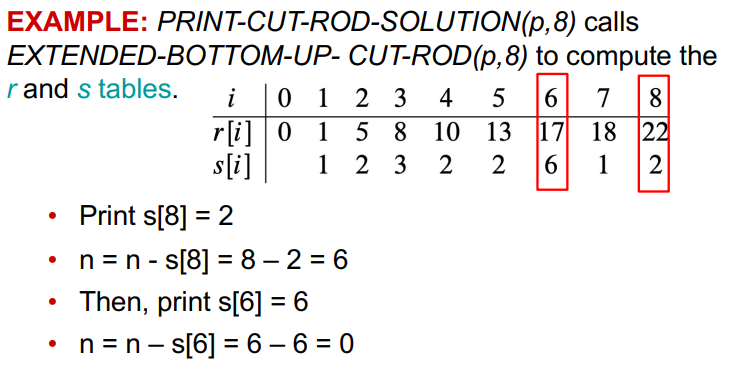
이렇게 코드를 짜면, s[n]은 처음으로 잘라지는 부분이며, 나머지 부분은 n-s[n] 값으로 table에서 다시 찾아주면 된다. 예시를 통해 좀 더 명확하게 이해해볼 수 있다.(↓)
'Computer Science > algorithms' 카테고리의 다른 글
| [알고리즘] Greedy algorithms (0) | 2021.10.27 |
|---|---|
| [알고리즘] Knapsack problem:dynamic programming (1) | 2021.10.14 |
| [알고리즘] LCS(The longest common subsequence)-dynamic programming (0) | 2021.10.10 |
| [알고리즘] Dynamic programming (0) | 2021.10.10 |
| [알고리즘] Binary search: divide-and-conquer (0) | 2021.10.10 |
